Question Number 143962 by lapache last updated on 20/Jun/21
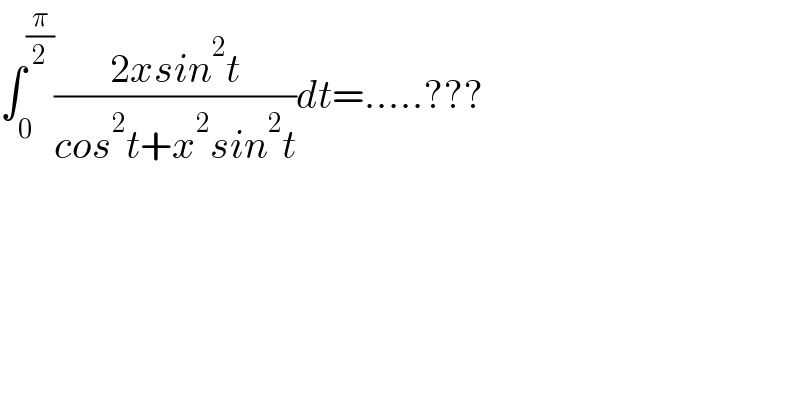
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{xsin}^{\mathrm{2}} {t}}{{cos}^{\mathrm{2}} {t}+{x}^{\mathrm{2}} {sin}^{\mathrm{2}} {t}}{dt}=…..??? \\ $$
Answered by Dwaipayan Shikari last updated on 20/Jun/21

$$\frac{\mathrm{2}}{{x}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}^{\mathrm{2}} {sin}^{\mathrm{2}} {t}}{{cos}^{\mathrm{2}} {t}+{x}^{\mathrm{2}} {sin}^{\mathrm{2}} {t}}{dt} \\ $$$$=\frac{\mathrm{2}}{{x}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{1}−\frac{{cos}^{\mathrm{2}} {t}}{{cos}^{\mathrm{2}} {t}+{x}^{\mathrm{2}} {sin}^{\mathrm{2}} {t}}{dt}=\frac{\pi}{{x}}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} {tan}^{\mathrm{2}} {t}}{dt} \\ $$$$=\frac{\pi}{{x}}−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+\left({xu}\right)^{\mathrm{2}} \right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{du} \\ $$$$=\frac{\pi}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} {u}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$=\frac{\pi}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}\left(\frac{\pi}{\mathrm{2}{x}}−\frac{\pi}{\mathrm{2}}\right)=\frac{\pi}{{x}}−\frac{\pi}{\mathrm{2}{x}\left({x}+\mathrm{1}\right)}=\frac{\pi}{\mathrm{2}{x}}+\frac{\pi}{\left(\mathrm{2}{x}+\mathrm{1}\right)} \\ $$
Commented by mnjuly1970 last updated on 20/Jun/21

$$\:{please}\:{rechech}\:{pen}−{ultimate}\:\:{line} \\ $$$$\:\:\:\left(\:{coefficient}\:\right) \\ $$
Answered by ArielVyny last updated on 20/Jun/21

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\frac{{cos}^{\mathrm{2}} {t}+{x}^{\mathrm{2}} {sin}^{\mathrm{2}} {t}}{\mathrm{2}{xsin}^{\mathrm{2}} {t}}}{dt} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}{x}}×\frac{\mathrm{1}}{{tan}^{\mathrm{2}} {t}}+\frac{{x}}{\mathrm{2}}}{dt}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\frac{\mathrm{1}}{{xtan}^{\mathrm{2}} {t}}+{x}}{dt} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\frac{\mathrm{1}+\left({xtant}\right)^{\mathrm{2}} }{{xtan}^{\mathrm{2}} {t}}}=\mathrm{2}{x}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{tan}^{\mathrm{2}} {t}}{\mathrm{1}+{x}^{\mathrm{2}} {tan}^{\mathrm{2}} {t}}{dt} \\ $$$$ \\ $$
