0-pi-2-cos-2-t-sint-dt-

Question Number 142643 by ArielVyny last updated on 03/Jun/21

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{2}} {t}}{{sint}}{dt} \\ $$

Answered by MJS_new last updated on 03/Jun/21

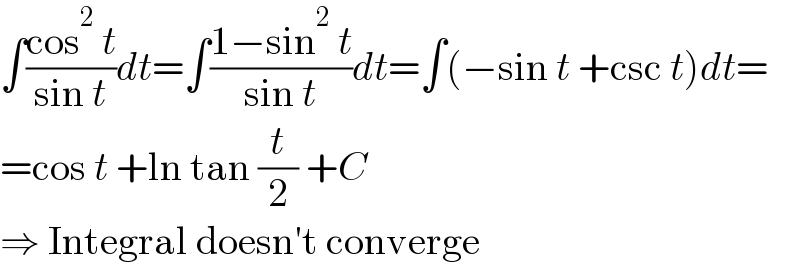
∫((cos^2 t)/(sin t))dt=∫((1−sin^2 t)/(sin t))dt=∫(−sin t +csc t)dt= =cos t +ln tan (t/2) +C ⇒ Integral doesn′t converge

$$\int\frac{\mathrm{cos}^{\mathrm{2}} \:{t}}{\mathrm{sin}\:{t}}{dt}=\int\frac{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{t}}{\mathrm{sin}\:{t}}{dt}=\int\left(−\mathrm{sin}\:{t}\:+\mathrm{csc}\:{t}\right){dt}= \\ $$$$=\mathrm{cos}\:{t}\:+\mathrm{ln}\:\mathrm{tan}\:\frac{{t}}{\mathrm{2}}\:+{C} \\ $$$$\Rightarrow\:\mathrm{Integral}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{converge} \\ $$

Commented by ArielVyny last updated on 03/Jun/21

in [0.(π/2)] integral does not converge ?

$${in}\:\left[\mathrm{0}.\frac{\pi}{\mathrm{2}}\right]\:{integral}\:{does}\:{not}\:{converge}\:? \\ $$

Commented by MJS_new last updated on 03/Jun/21

yes. [cos x]_0 ^(π/2) =0−1=−1 [ln tan (x/2)]_0 ^(π/2) =0−lim_(x→0^+ ) ln tan (x/2) but this limit doesn′t exist

$$\mathrm{yes}. \\ $$$$\left[\mathrm{cos}\:{x}\overset{\pi/\mathrm{2}} {\right]}_{\mathrm{0}} =\mathrm{0}−\mathrm{1}=−\mathrm{1} \\ $$$$\left[\mathrm{ln}\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} =\mathrm{0}−\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\mathrm{ln}\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\:\:\:\:\mathrm{but}\:\mathrm{this}\:\mathrm{limit}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$

Facebook Tweet Pin

0-pi-2-cos-2-t-sint-dt-

Leave a Reply Cancel reply