Question Number 135851 by Ñï= last updated on 16/Mar/21
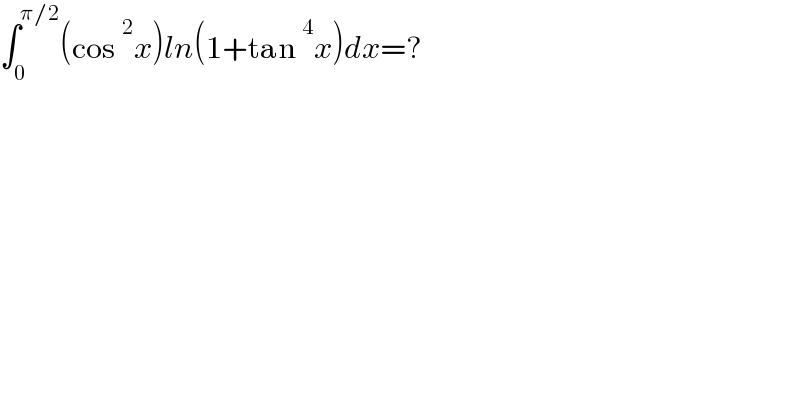
$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{cos}\:^{\mathrm{2}} {x}\right){ln}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}\right){dx}=? \\ $$
Answered by mathmax by abdo last updated on 16/Mar/21

$$\mathrm{let}\:\Phi=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{x}.\mathrm{log}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{4}} \mathrm{x}\right)\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}} \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{channgement}\:\mathrm{tanx}=\mathrm{t}\:\Rightarrow \\ $$$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{log}\left(\mathrm{1}+\mathrm{t}^{\mathrm{4}} \right)\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{t}^{\mathrm{4}} \right)}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}\:\mathrm{let} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{at}^{\mathrm{4}} \right)}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}\:\:\:\left(\mathrm{a}\geqslant\mathrm{0}\right)\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{4}} }{\left(\mathrm{at}^{\mathrm{4}} \:+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{t}^{\mathrm{4}} }{\mathrm{a}\left(\mathrm{t}^{\mathrm{4}} \:+\left(\mathrm{a}^{\frac{\mathrm{1}}{\mathrm{4}}} \right)^{\mathrm{4}} \right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}\:\left(\mathrm{x}_{\mathrm{0}} =\mathrm{a}^{\frac{\mathrm{1}}{\mathrm{4}}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2a}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{t}^{\mathrm{4}} }{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{ix}_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} +\mathrm{ix}_{\mathrm{0}} ^{\mathrm{2}} \right)\left(\mathrm{t}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{t}+\mathrm{i}\right)^{\mathrm{2}} \right.}\mathrm{dt}\:\Rightarrow \\ $$$$\mathrm{2af}^{'} \left(\mathrm{a}\right)\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{t}^{\mathrm{4}} }{\left(\mathrm{t}−\mathrm{x}_{\mathrm{0}} \mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{t}+\mathrm{x}_{\mathrm{0}} \mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{t}−\mathrm{x}_{\mathrm{0}} \mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{t}+\mathrm{x}_{\mathrm{0}} \mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{t}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{t}+\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2i}\pi\left\{\mathrm{Res}\left(\mathrm{w},\mathrm{x}_{\mathrm{0}} \mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)+\mathrm{Res}\left(\mathrm{w},−\mathrm{x}_{\mathrm{0}} \mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)+\mathrm{Res}\left(\mathrm{w},\mathrm{i}\right)\right\} \\ $$$$\mathrm{Res}\left(\mathrm{w},\mathrm{x}_{\mathrm{0}} \mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\:=\frac{−\mathrm{x}_{\mathrm{0}} ^{\mathrm{4}} }{\mathrm{2x}_{\mathrm{0}} \mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \left(\mathrm{x}_{\mathrm{0}} ^{\mathrm{2}} \mathrm{i}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Res}\left(\mathrm{w},−\mathrm{x}_{\mathrm{0}} \mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\:=\frac{−\mathrm{x}_{\mathrm{0}} ^{\mathrm{4}} }{−\mathrm{2x}_{\mathrm{0}} \mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \left(−\mathrm{ix}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Res}\left(\mathrm{w},\mathrm{i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\left\{\frac{\mathrm{t}^{\mathrm{4}} }{\left(\mathrm{t}^{\mathrm{4}} \:+\mathrm{x}_{\mathrm{0}} ^{\mathrm{4}} \right)\left(\mathrm{t}+\mathrm{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \:=…. \\ $$$$…\mathrm{be}\:\mathrm{continued}…. \\ $$
Commented by mathmax by abdo last updated on 16/Mar/21
![let try another way Φ=∫_0 ^∞ ((log(1+t^4 ))/((t^2 +1)^2 ))dt ⇒ Φ=_(t=(1/x)) −∫_0 ^∞ ((log(1+(1/x^2 )))/(((1/x^2 )+1)^2 ))(−(dx/x^2 )) =∫_0 ^∞ x^4 ((log(1+x^2 )−2logx)/(x^2 (1+x^2 )^2 )) =∫_0 ^∞ (x^2 /((1+x^2 )^2 ))(log(1+x^2 )−2logx)dx =∫_0 ^∞ ((x^2 log(1+x^2 ))/((1+x^2 )^2 ))dx−2 ∫_0 ^∞ ((x^2 logx)/((1+x^2 )^2 ))dx=H−2K we have H=∫_0 ^∞ ((x^2 log(1+x^2 ))/((1+x^2 )^2 ))dx =∫_0 ^∞ (x/((1+x^2 )^2 ))(xlog(1+x^2 ))dx by parts u^′ =(x/((1+x^2 )^2 )) ⇒u =−(1/(2(1+x^2 ))) and v=xlog(1+x^2 ) ⇒ H =[−(1/(2(1+x^2 )))xlog(1+x^2 )]_0 ^∞ +∫_0 ^∞ (1/(2(1+x^2 )))(log(1+x^2 )+((2x^2 )/(1+x^2 )))dx =(1/2)∫_0 ^∞ ((log(1+x^2 ))/(1+x^2 ))dx+∫_0 ^∞ (x^2 /(2(1+x^2 )^2 ))dx ∫_0 ^∞ ((log(1+x^2 ))/(1+x^2 ))dx =_(x=tanθ) ∫_0 ^(π/2) ((log((1/(cos^2 θ))))/(1+tan^2 θ))(1+tan^2 θ)dθ =−2∫_0 ^(π/2) log(cosθ)dθ =−2(−(π/2)log2)=πlog2 ∫_0 ^∞ (x^2 /(2(1+x^2 )^2 ))dx =∫_0 ^∞ ((1+x^2 −1)/(2(1+x^2 )^2 ))dx =(1/2)∫_0 ^∞ (dx/(1+x^2 ))−(1/2)∫_0 ^∞ (dx/((1+x^2 )^2 ))(x=tanθ) =(π/4)−(1/2)∫_0 ^(π/2) ((1+tan^2 θ)/((1+tan^2 θ)^2 ))dθ =(π/4)−(1/2)∫_0 ^(π/2) cos^2 θdθ =(π/4)−(1/4)∫_0 ^(π/2) (1+cos(2θ))dθ =(π/4)−(π/8)−(1/8)[sin(2θ)]_0 ^(π/2) =(π/8) ⇒ H =(π/2)log(2)+(π/8) K =∫_0 ^∞ ((x^2 logx)/((1+x^2 )^2 ))dx =∫_0 ^∞ (((x^2 +1−1)logx)/((x^2 +1)^2 ))dx =∫_0 ^∞ ((logx)/(1+x^2 ))dx(=0)−∫_0 ^∞ ((logx)/((x^2 +1)^2 ))dx we have ∫_0 ^∞ ((logx)/((1+x^2 )^2 ))dx =∫_0 ^1 ((logx)/((1+x^2 )^2 ))dx+∫_1 ^∞ ((logx)/((1+x^2 )^2 ))dx(x=(1/t)) =∫_0 ^1 ((logx)/((1+x^2 )^2 ))dx −∫_0 ^1 ((−logt)/((1+(1/t^2 ))^2 ))(−(dt/t^2 ) =∫_0 ^1 ((logx)/((1+x^2 )^2 ))dx−∫_0 ^1 ((t^2 logt)/((t^2 +1)^2 ))dt we have (1/(1+x^2 ))=Σ_(n=0) ^∞ (−1)^n x^(2n) ⇒ ((−2x)/((1+x^2 )^2 )) =Σ_(n=1) ^∞ 2n(−1)^n x^(2n−1) ⇒(1/((1+x^2 )^2 )) =Σ_(n=1) ^∞ n(−1)^(n−1) x^(2n−2) ⇒ ∫_0 ^1 ((logx)/((1+x^2 )^2 ))dx =Σ_(n=1) ^∞ n(−1)^n (1/(2n−1)) ...be continued....](https://www.tinkutara.com/question/Q135882.png)
$$\mathrm{let}\:\mathrm{try}\:\mathrm{another}\:\mathrm{way}\:\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{t}^{\mathrm{4}} \right)}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}\:\Rightarrow \\ $$$$\Phi=_{\mathrm{t}=\frac{\mathrm{1}}{\mathrm{x}}} \:\:\:\:−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)}{\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{1}\right)^{\mathrm{2}} }\left(−\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} }\right)\:=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{4}} \:\:\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)−\mathrm{2logx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\left(\mathrm{log}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)−\mathrm{2logx}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{log}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}−\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{logx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\mathrm{H}−\mathrm{2K}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{H}=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{log}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\left(\mathrm{xlog}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\right)\mathrm{dx} \\ $$$$\mathrm{by}\:\mathrm{parts}\:\:\mathrm{u}^{'} =\frac{\mathrm{x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow\mathrm{u}\:=−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\:\mathrm{and}\:\mathrm{v}=\mathrm{xlog}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\mathrm{H}\:=\left[−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{xlog}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\left(\mathrm{log}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)+\frac{\mathrm{2x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}+\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{x}=\mathrm{tan}\theta} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{log}\left(\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \theta}\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)\mathrm{d}\theta \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{log}\left(\mathrm{cos}\theta\right)\mathrm{d}\theta\:=−\mathrm{2}\left(−\frac{\pi}{\mathrm{2}}\mathrm{log2}\right)=\pi\mathrm{log2} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\left(\mathrm{x}=\mathrm{tan}\theta\right) \\ $$$$=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\mathrm{d}\theta\:=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)\right)\mathrm{d}\theta\:=\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}}\left[\mathrm{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\pi}{\mathrm{8}}\:\Rightarrow\:\mathrm{H}\:=\frac{\pi}{\mathrm{2}}\mathrm{log}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{8}} \\ $$$$\mathrm{K}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{logx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}\right)\mathrm{logx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\left(=\mathrm{0}\right)−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{logx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}+\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{logx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\left(\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\mathrm{logt}}{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }\left(−\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right. \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{t}^{\mathrm{2}} \mathrm{logt}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} \:\Rightarrow \\ $$$$\frac{−\mathrm{2x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{2n}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}−\mathrm{1}} \:\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}−\mathrm{2}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{2n}−\mathrm{1}}\:\:\:…\mathrm{be}\:\mathrm{continued}…. \\ $$
Commented by Ñï= last updated on 16/Mar/21
![∫_0 ^(π/2) (cos^2 x)ln(1+tan^4 x)dx =^(x→(π/2)−x) ∫_0 ^(π/2) (sin^2 x)ln(1+tan^4 x)dx−4∫_0 ^(π/2) (sin^2 x)ln(tan x)dx ∫_0 ^(π/2) (cos^2 x)ln(1+tan^4 x)dx−∫_0 ^(π/2) (sin^2 x)ln(1+tan^4 x)dx=−4∫_0 ^(π/2) (sin^2 x)ln(tan x)dx=−π ∫_0 ^(π/2) (cos^2 x)ln(1+tan^4 x)dx+∫_0 ^(π/2) (sin^2 x)ln(1+tan^4 x)dx=∫_0 ^(π/2) ln(1+tan^4 x)dx=(π/2)ln(6+4(√2)) ∫_0 ^(π/2) (cos^2 x)ln(1+tan^4 x)dx=(1/2)[−π+(π/2)ln(6+4(√2))] ∫_0 ^(π/2) (sin^2 x)ln(1+tan^4 x)dx=(1/2)[π+(π/2)ln(6+4(√2))]](https://www.tinkutara.com/question/Q135885.png)
$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{cos}\:^{\mathrm{2}} {x}\right){ln}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}\right){dx} \\ $$$$\overset{{x}\rightarrow\frac{\pi}{\mathrm{2}}−{x}} {=}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{sin}\:^{\mathrm{2}} {x}\right){ln}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}\right){dx}−\mathrm{4}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{sin}\:^{\mathrm{2}} {x}\right){ln}\left(\mathrm{tan}\:{x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({cos}\:^{\mathrm{2}} {x}\right){ln}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}\right){dx}−\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{sin}\:^{\mathrm{2}} {x}\right){ln}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}\right){dx}=−\mathrm{4}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{sin}\:^{\mathrm{2}} {x}\right){ln}\left(\mathrm{tan}\:{x}\right){dx}=−\pi \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({cos}\:^{\mathrm{2}} {x}\right){ln}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}\right){dx}+\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{sin}\:^{\mathrm{2}} {x}\right){ln}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}\right){dx}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {ln}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}\right){dx}=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{6}+\mathrm{4}\sqrt{\mathrm{2}}\right) \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({cos}\:^{\mathrm{2}} {x}\right){ln}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\left[−\pi+\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{6}+\mathrm{4}\sqrt{\mathrm{2}}\right)\right] \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{sin}\:^{\mathrm{2}} {x}\right){ln}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\left[\pi+\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{6}+\mathrm{4}\sqrt{\mathrm{2}}\right)\right] \\ $$
Commented by mathmax by abdo last updated on 16/Mar/21

$$\mathrm{from}\:\mathrm{where}\:\mathrm{come}\:−\pi\:\mathrm{and}\:\mathrm{sign}\:+\:\mathrm{sir}? \\ $$
Commented by Ajetunmobi last updated on 17/Mar/21
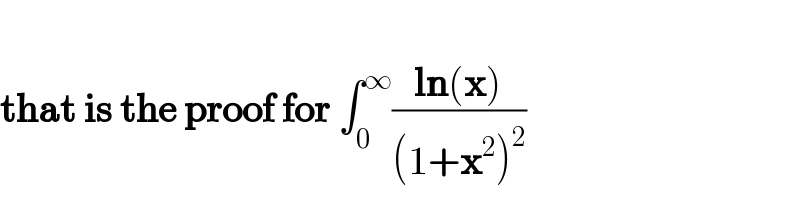
$$ \\ $$$$\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{proof}}\:\boldsymbol{\mathrm{for}}\:\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)}{\left(\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$
Commented by Ajetunmobi last updated on 16/Mar/21

Commented by Ajetunmobi last updated on 17/Mar/21

$$ \\ $$$$\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{proposal}} \\ $$$$\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{u}}\:\boldsymbol{\mathrm{show}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{full}}\:\boldsymbol{\mathrm{solution}}\:? \\ $$$$\boldsymbol{\mathrm{because}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{integral}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{somehow}}\:\boldsymbol{\mathrm{elegant}}\:\boldsymbol{\mathrm{and}}\: \\ $$$$\boldsymbol{\mathrm{also}}\:\boldsymbol{\mathrm{lenghty}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{my}}\:\boldsymbol{\mathrm{view}} \\ $$
Commented by mathmax by abdo last updated on 17/Mar/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 17/Mar/21

$$\mathrm{let}\:\mathrm{use}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{p}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\Sigma\mathrm{Res}\:\left(\mathrm{p}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \left(\mathrm{z}\right),\mathrm{a}_{\mathrm{i}} \right)\:\mathrm{we}\:\mathrm{have}\right. \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$\Sigma\:\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{i}} \right)\:=\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:+\mathrm{Res}\left(\varphi,−\mathrm{i}\right) \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\frac{\mathrm{2lnz}}{\mathrm{z}}\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} } \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\frac{\frac{\mathrm{2lnz}}{\mathrm{z}}\left(\mathrm{z}+\mathrm{i}\right)−\mathrm{2ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} }\:=\frac{\mathrm{4lni}−\mathrm{2ln}^{\mathrm{2}} \mathrm{i}}{\left(\mathrm{2i}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{4ln}\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)−\mathrm{2}\left(\mathrm{ln}\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)\right)^{\mathrm{2}} }{−\mathrm{8i}}=\frac{\mathrm{2i}\pi−\mathrm{2}\left(\frac{\mathrm{i}\pi}{\mathrm{2}}\right)^{\mathrm{2}} }{−\mathrm{8i}}=−\frac{\mathrm{2i}\pi−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}}{\mathrm{8i}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(−\mathrm{2}\pi−\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{2}}\right)=−\frac{\pi}{\mathrm{4}}−\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\mathrm{Res}\left(\varphi,−\mathrm{i}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{i}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{i}} \:\:\:\frac{\frac{\mathrm{2lnz}}{\mathrm{z}}\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{z}−\mathrm{i}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{4}} } \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{i}} \:\:\:\:\frac{\frac{\mathrm{2lnz}}{\mathrm{z}}\left(\mathrm{z}−\mathrm{i}\right)−\mathrm{2ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{3}} }=\frac{\mathrm{4ln}\left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)−\mathrm{2}\left(\mathrm{ln}\left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)\right)^{\mathrm{2}} }{\left(−\mathrm{2i}\right)^{\mathrm{3}} } \\ $$$$=\frac{−\mathrm{2i}\pi−\mathrm{2}\left(−\frac{\mathrm{i}\pi}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{8i}}\:=\frac{−\mathrm{2i}\pi−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}}{\mathrm{8i}}=−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\Rightarrow\Sigma\:\mathrm{Res}\left(\varphi\:,\mathrm{z}_{\mathrm{i}} \right)\:=−\frac{\pi}{\mathrm{2}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\pi}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{4}} \\ $$
Commented by Ajetunmobi last updated on 17/Mar/21

$$\boldsymbol{\mathrm{welcome}}\:\boldsymbol{\mathrm{sir}} \\ $$
Commented by Ajetunmobi last updated on 17/Mar/21

$$\boldsymbol{\mathrm{I}}\:\boldsymbol{\mathrm{dont}}\:\boldsymbol{\mathrm{know}}\:\boldsymbol{\mathrm{residue}}\:\boldsymbol{\mathrm{theorem}}\:\boldsymbol{\mathrm{though}}\: \\ $$$$\boldsymbol{\mathrm{but}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{answer}}\:\boldsymbol{\mathrm{is}}\:\:−\frac{\boldsymbol{\pi}}{\mathrm{4}} \\ $$
Commented by Ajetunmobi last updated on 17/Mar/21

$$\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{answer}}\:\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{proposal}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{correct}}\: \\ $$$$\boldsymbol{\mathrm{but}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{dont}}\:\boldsymbol{\mathrm{really}}\:\boldsymbol{\mathrm{understand}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{solution}}\: \\ $$$$\boldsymbol{\mathrm{because}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{proposal}}\:\boldsymbol{\mathrm{never}}\:\boldsymbol{\mathrm{show}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{full}} \\ $$$$\boldsymbol{\mathrm{solution}} \\ $$
