Question Number 138077 by mohammad17 last updated on 09/Apr/21
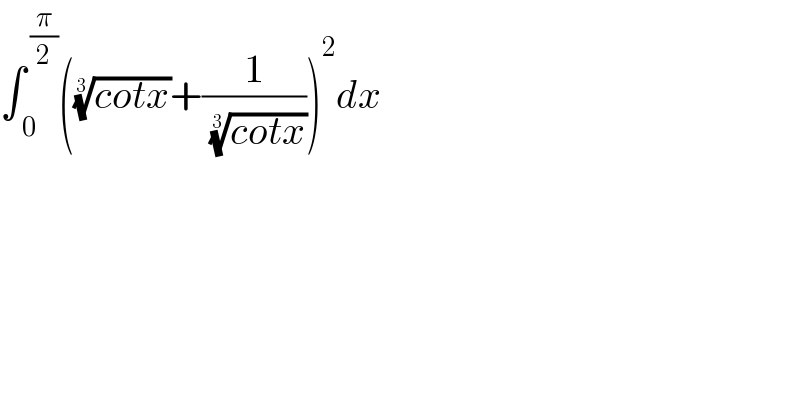
$$\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \left(\sqrt[{\mathrm{3}}]{{cotx}}+\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{cotx}}}\right)^{\mathrm{2}} {dx} \\ $$
Answered by Dwaipayan Shikari last updated on 09/Apr/21
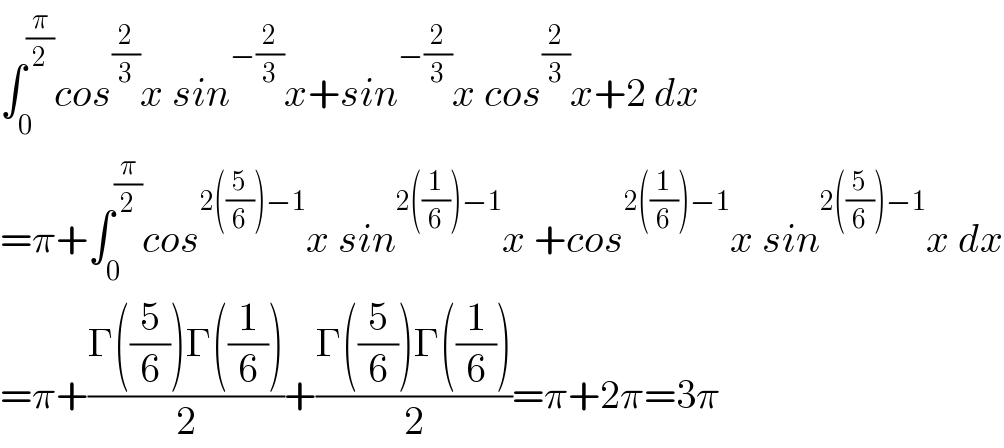
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\frac{\mathrm{2}}{\mathrm{3}}} {x}\:{sin}^{−\frac{\mathrm{2}}{\mathrm{3}}} {x}+{sin}^{−\frac{\mathrm{2}}{\mathrm{3}}} {x}\:{cos}^{\frac{\mathrm{2}}{\mathrm{3}}} {x}+\mathrm{2}\:{dx} \\ $$$$=\pi+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}\left(\frac{\mathrm{5}}{\mathrm{6}}\right)−\mathrm{1}} {x}\:{sin}^{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{6}}\right)−\mathrm{1}} {x}\:+{cos}^{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{6}}\right)−\mathrm{1}} {x}\:{sin}^{\mathrm{2}\left(\frac{\mathrm{5}}{\mathrm{6}}\right)−\mathrm{1}} {x}\:{dx} \\ $$$$=\pi+\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{6}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)}{\mathrm{2}}+\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{6}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)}{\mathrm{2}}=\pi+\mathrm{2}\pi=\mathrm{3}\pi \\ $$
Answered by mathmax by abdo last updated on 10/Apr/21

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\:\left(\mathrm{cotanx}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:+\left(\mathrm{tanx}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right)^{\mathrm{2}} \:\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{cosx}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:\mathrm{sinx}^{−\frac{\mathrm{2}}{\mathrm{3}}} \:\mathrm{dx}\:+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{dx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{sinx}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:\left(\mathrm{cosx}\right)^{−\frac{\mathrm{2}}{\mathrm{3}}} \:\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{know}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2p}−\mathrm{1}} \mathrm{x}\:\mathrm{sin}^{\mathrm{2q}−\mathrm{1}} \mathrm{x}\:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{B}\left(\mathrm{p},\mathrm{q}\right)=\frac{\Gamma\left(\mathrm{p}\right)\Gamma\left(\mathrm{q}\right)}{\Gamma\left(\mathrm{p}+\mathrm{q}\right)} \\ $$$$\mathrm{2p}−\mathrm{1}=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\mathrm{2p}=\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{3}}\:\Rightarrow\mathrm{p}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\mathrm{2q}−\mathrm{1}=−\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\mathrm{2q}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\mathrm{q}=\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{cosx}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:\left(\mathrm{sinx}\right)^{−\frac{\mathrm{2}}{\mathrm{3}}} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{B}\left(\frac{\mathrm{5}}{\mathrm{6}},\frac{\mathrm{1}}{\mathrm{6}}\right)\:=\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{6}}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)}{\mathrm{2}\Gamma\left(\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right).\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{6}}\right)}\:=\frac{\pi}{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}}=\pi\:\:\mathrm{duo}\:\mathrm{to}\:\mathrm{symetrie}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{sinx}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:\left(\mathrm{cosx}\right)^{−\frac{\mathrm{2}}{\mathrm{3}}} \:\mathrm{dx}\:=\pi\:\Rightarrow \\ $$$$\mathrm{I}=\pi+\pi\:+\pi\:=\mathrm{3}\pi \\ $$
