Menu Close

0-pi-2-sin-40x-sin-5x-dx-

Tinku Tara 0 Comments
Pin




Question Number 141998 by iloveisrael last updated on 25/May/21
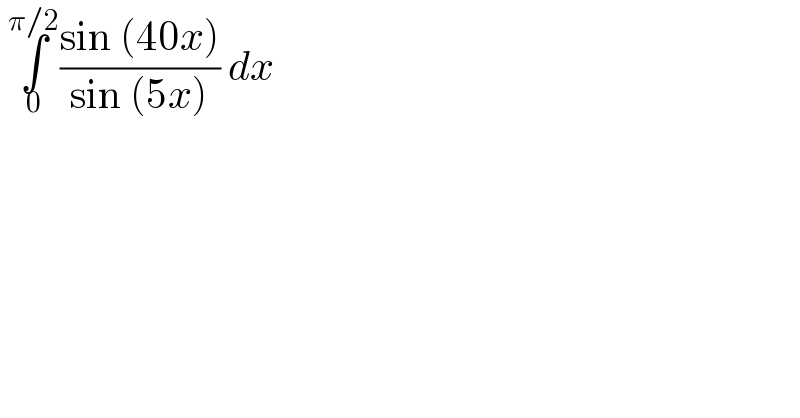
∫_0 ^(π/2) ((sin (40x))/(sin (5x))) dx
$$\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{sin}\:\left(\mathrm{40}{x}\right)}{\mathrm{sin}\:\left(\mathrm{5}{x}\right)}\:{dx}\: \\ $$
Answered by EDWIN88 last updated on 25/May/21
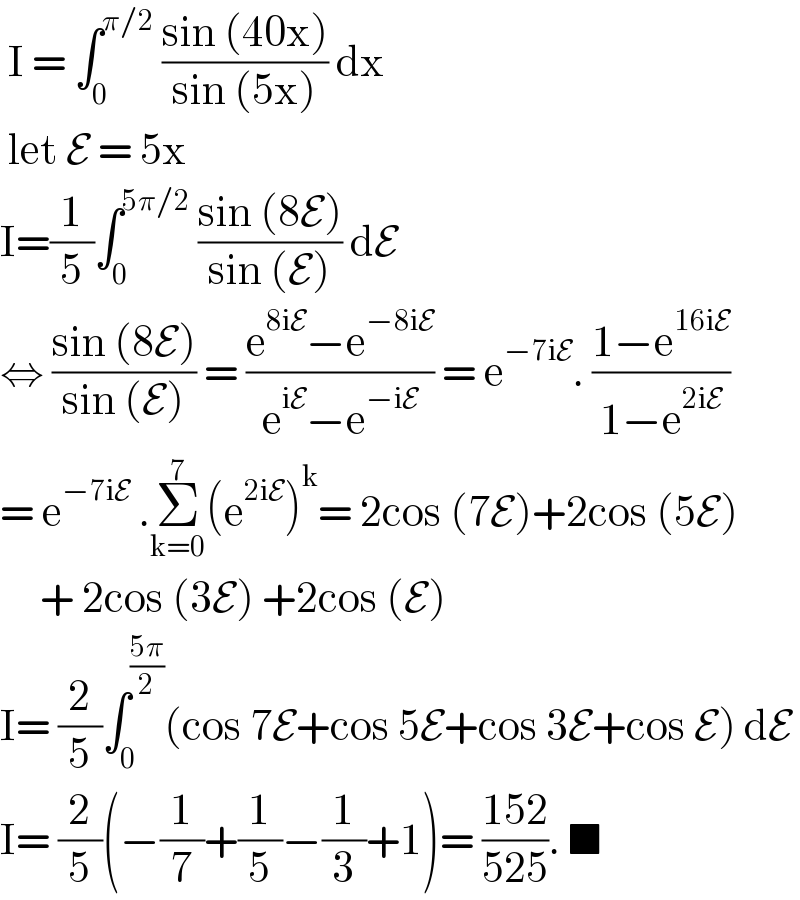
I = ∫_0 ^(π/2) ((sin (40x))/(sin (5x))) dx let E = 5x I=(1/5)∫_0 ^(5π/2) ((sin (8E))/(sin (E))) dE ⇔ ((sin (8E))/(sin (E))) = ((e^(8iE) −e^(−8iE) )/(e^(iE) −e^(−iE) )) = e^(−7iE) . ((1−e^(16iE) )/(1−e^(2iE) )) = e^(−7iE) .Σ_(k=0) ^7 (e^(2iE) )^k = 2cos (7E)+2cos (5E) + 2cos (3E) +2cos (E) I= (2/5)∫_0 ^((5π)/2) (cos 7E+cos 5E+cos 3E+cos E) dE I= (2/5)(−(1/7)+(1/5)−(1/3)+1)= ((152)/(525)). ■
$$\:\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\frac{\mathrm{sin}\:\left(\mathrm{40x}\right)}{\mathrm{sin}\:\left(\mathrm{5x}\right)}\:\mathrm{dx}\: \\ $$$$\:\mathrm{let}\:\mathcal{E}\:=\:\mathrm{5x}\: \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{5}}\int_{\mathrm{0}} ^{\mathrm{5}\pi/\mathrm{2}} \:\frac{\mathrm{sin}\:\left(\mathrm{8}\mathcal{E}\right)}{\mathrm{sin}\:\left(\mathcal{E}\right)}\:\mathrm{d}\mathcal{E}\: \\ $$$$\Leftrightarrow\:\frac{\mathrm{sin}\:\left(\mathrm{8}\mathcal{E}\right)}{\mathrm{sin}\:\left(\mathcal{E}\right)}\:=\:\frac{\mathrm{e}^{\mathrm{8i}\mathcal{E}} −\mathrm{e}^{−\mathrm{8i}\mathcal{E}} }{\mathrm{e}^{\mathrm{i}\mathcal{E}} −\mathrm{e}^{−\mathrm{i}\mathcal{E}} }\:=\:\mathrm{e}^{−\mathrm{7i}\mathcal{E}} .\:\frac{\mathrm{1}−\mathrm{e}^{\mathrm{16i}\mathcal{E}} }{\mathrm{1}−\mathrm{e}^{\mathrm{2i}\mathcal{E}} } \\ $$$$=\:\mathrm{e}^{−\mathrm{7i}\mathcal{E}} \:.\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\left(\mathrm{e}^{\mathrm{2i}\mathcal{E}} \right)^{\mathrm{k}} =\:\mathrm{2cos}\:\left(\mathrm{7}\mathcal{E}\right)+\mathrm{2cos}\:\left(\mathrm{5}\mathcal{E}\right) \\ $$$$\:\:\:\:\:+\:\mathrm{2cos}\:\left(\mathrm{3}\mathcal{E}\right)\:+\mathrm{2cos}\:\left(\mathcal{E}\right) \\ $$$$\mathrm{I}=\:\frac{\mathrm{2}}{\mathrm{5}}\int_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \left(\mathrm{cos}\:\mathrm{7}\mathcal{E}+\mathrm{cos}\:\mathrm{5}\mathcal{E}+\mathrm{cos}\:\mathrm{3}\mathcal{E}+\mathrm{cos}\:\mathcal{E}\right)\:\mathrm{d}\mathcal{E} \\ $$$$\mathrm{I}=\:\frac{\mathrm{2}}{\mathrm{5}}\left(−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}\right)=\:\frac{\mathrm{152}}{\mathrm{525}}.\:\blacksquare \\ $$
Answered by mathmax by abdo last updated on 26/May/21
Ψ=∫_0 ^(π/2) ((sin(40x))/(sin(5x)))dx changement 5x=t give Ψ=(1/5)∫_0 ^((5π)/2) ((sin(8t))/(sint))dt ⇒5Ψ=∫_0 ^((5π)/2) ((2sin(4t)cos(4t))/(sint))dt =2 ∫_0 ^((5π)/2) ((2sin(2t)cos(2t)cos(4t))/(sint))dt =4 ∫_0 ^((5π)/2) ((2sint cost cos(2t)cos(4t))/(sint))dt =8 ∫_0 ^((5π)/2) cost cos(2t)cos(4t) dt =4∫_0 ^((5π)/2) (cos(3t)+cost)cos(4t)dt =4 ∫_0 ^((5π)/2) cos(3t)cos(4t)+4 ∫_0 ^((5π)/2) cost cos(4t)dt =2∫_0 ^((5π)/2) (cos(7t)+cost)dt +2∫_0 ^((5π)/2) (cos(5t)+cos(3t))dt =2[(1/7)sin(7t)+sint]_0 ^((5π)/2) +2[(1/5)sin(5t)+(1/3)sin(3t)]_0 ^((5π)/2) no its eazy to get the results....
$$\Psi=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sin}\left(\mathrm{40x}\right)}{\mathrm{sin}\left(\mathrm{5x}\right)}\mathrm{dx}\:\mathrm{changement}\:\mathrm{5x}=\mathrm{t}\:\mathrm{give} \\ $$$$\Psi=\frac{\mathrm{1}}{\mathrm{5}}\int_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \:\frac{\mathrm{sin}\left(\mathrm{8t}\right)}{\mathrm{sint}}\mathrm{dt}\:\Rightarrow\mathrm{5}\Psi=\int_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \:\frac{\mathrm{2sin}\left(\mathrm{4t}\right)\mathrm{cos}\left(\mathrm{4t}\right)}{\mathrm{sint}}\mathrm{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \:\frac{\mathrm{2sin}\left(\mathrm{2t}\right)\mathrm{cos}\left(\mathrm{2t}\right)\mathrm{cos}\left(\mathrm{4t}\right)}{\mathrm{sint}}\mathrm{dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \:\frac{\mathrm{2sint}\:\mathrm{cost}\:\mathrm{cos}\left(\mathrm{2t}\right)\mathrm{cos}\left(\mathrm{4t}\right)}{\mathrm{sint}}\mathrm{dt} \\ $$$$=\mathrm{8}\:\int_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \:\mathrm{cost}\:\mathrm{cos}\left(\mathrm{2t}\right)\mathrm{cos}\left(\mathrm{4t}\right)\:\mathrm{dt} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \left(\mathrm{cos}\left(\mathrm{3t}\right)+\mathrm{cost}\right)\mathrm{cos}\left(\mathrm{4t}\right)\mathrm{dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \:\mathrm{cos}\left(\mathrm{3t}\right)\mathrm{cos}\left(\mathrm{4t}\right)+\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \:\mathrm{cost}\:\mathrm{cos}\left(\mathrm{4t}\right)\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \:\left(\mathrm{cos}\left(\mathrm{7t}\right)+\mathrm{cost}\right)\mathrm{dt}\:+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \left(\mathrm{cos}\left(\mathrm{5t}\right)+\mathrm{cos}\left(\mathrm{3t}\right)\right)\mathrm{dt} \\ $$$$=\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{7}}\mathrm{sin}\left(\mathrm{7t}\right)+\mathrm{sint}\right]_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} +\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{5}}\mathrm{sin}\left(\mathrm{5t}\right)+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\left(\mathrm{3t}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{5}\pi}{\mathrm{2}}} \\ $$$$\mathrm{no}\:\mathrm{its}\:\mathrm{eazy}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{results}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *