Question Number 139353 by mohammad17 last updated on 26/Apr/21
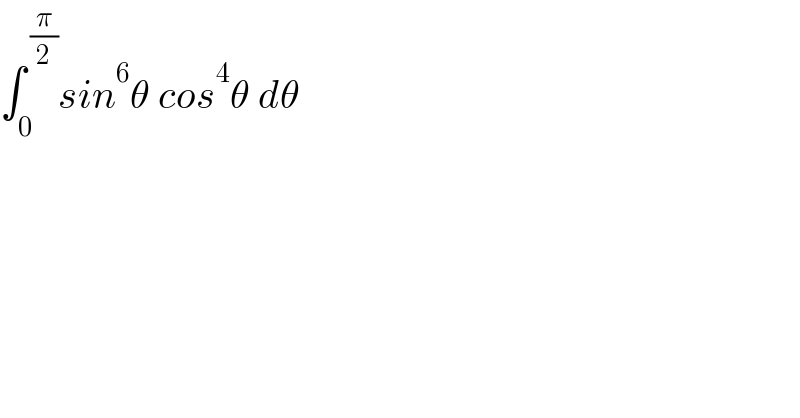
$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{6}} \theta\:{cos}^{\mathrm{4}} \theta\:{d}\theta \\ $$
Answered by Dwaipayan Shikari last updated on 26/Apr/21
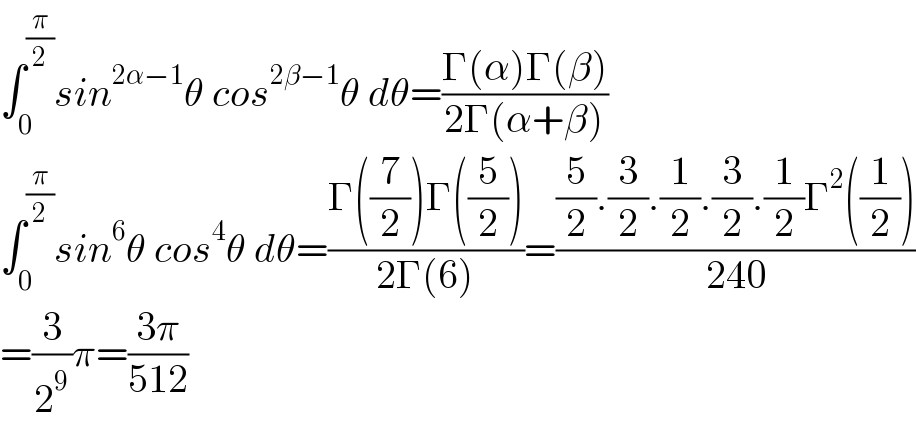
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}\alpha−\mathrm{1}} \theta\:{cos}^{\mathrm{2}\beta−\mathrm{1}} \theta\:{d}\theta=\frac{\Gamma\left(\alpha\right)\Gamma\left(\beta\right)}{\mathrm{2}\Gamma\left(\alpha+\beta\right)} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{6}} \theta\:{cos}^{\mathrm{4}} \theta\:{d}\theta=\frac{\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\mathrm{6}\right)}=\frac{\frac{\mathrm{5}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{240}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{9}} }\pi=\frac{\mathrm{3}\pi}{\mathrm{512}} \\ $$
Answered by ajfour last updated on 26/Apr/21
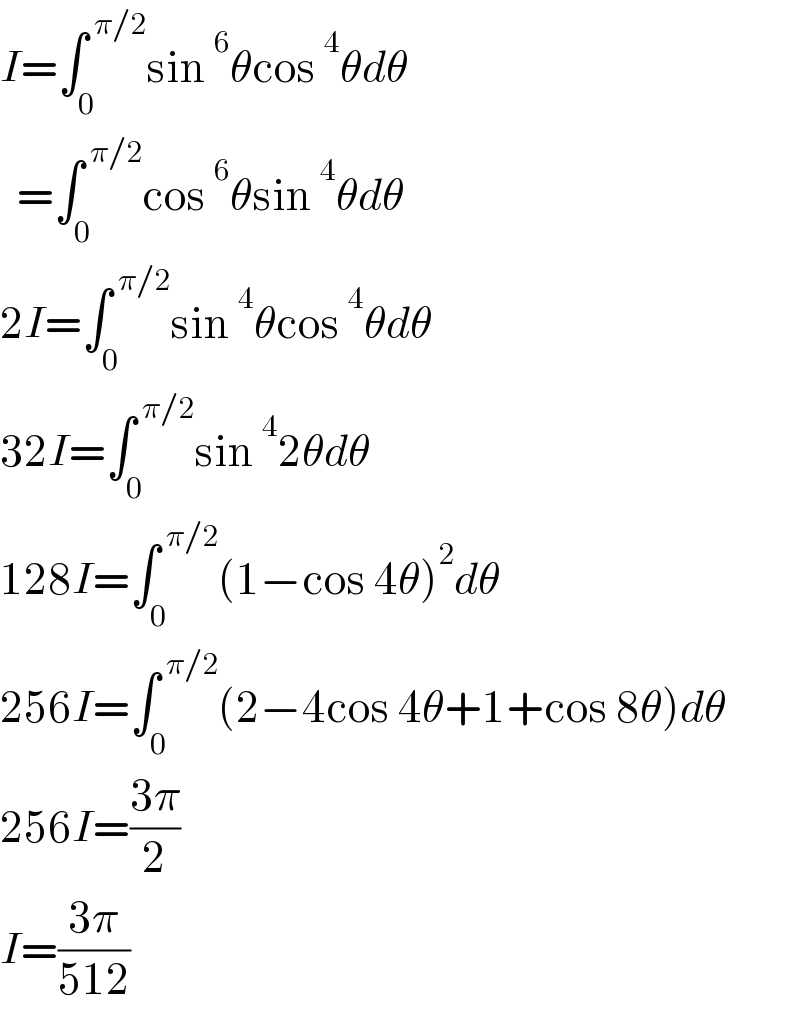
$${I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{sin}\:^{\mathrm{6}} \theta\mathrm{cos}\:^{\mathrm{4}} \theta{d}\theta \\ $$$$\:\:=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{cos}\:^{\mathrm{6}} \theta\mathrm{sin}\:^{\mathrm{4}} \theta{d}\theta \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{sin}\:^{\mathrm{4}} \theta\mathrm{cos}\:^{\mathrm{4}} \theta{d}\theta \\ $$$$\mathrm{32}{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{sin}\:^{\mathrm{4}} \mathrm{2}\theta{d}\theta \\ $$$$\mathrm{128}{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\mathrm{4}\theta\right)^{\mathrm{2}} {d}\theta \\ $$$$\mathrm{256}{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \left(\mathrm{2}−\mathrm{4cos}\:\mathrm{4}\theta+\mathrm{1}+\mathrm{cos}\:\mathrm{8}\theta\right){d}\theta \\ $$$$\mathrm{256}{I}=\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$${I}=\frac{\mathrm{3}\pi}{\mathrm{512}} \\ $$
