Question Number 137315 by liberty last updated on 01/Apr/21
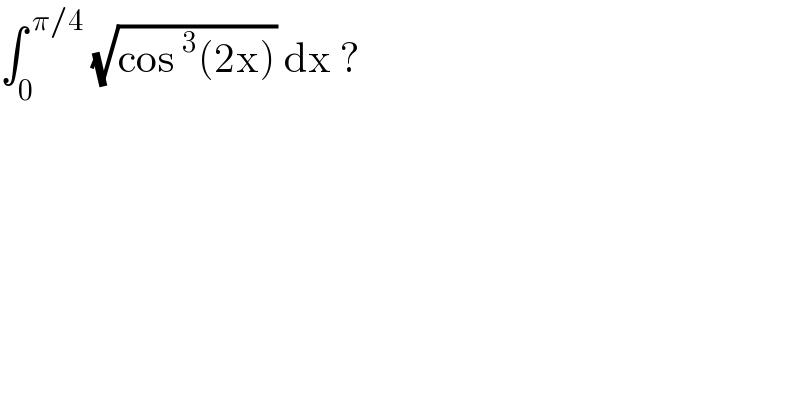
$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \:\sqrt{\mathrm{cos}\:^{\mathrm{3}} \left(\mathrm{2x}\right)}\:\mathrm{dx}\:? \\ $$
Answered by rs4089 last updated on 01/Apr/21
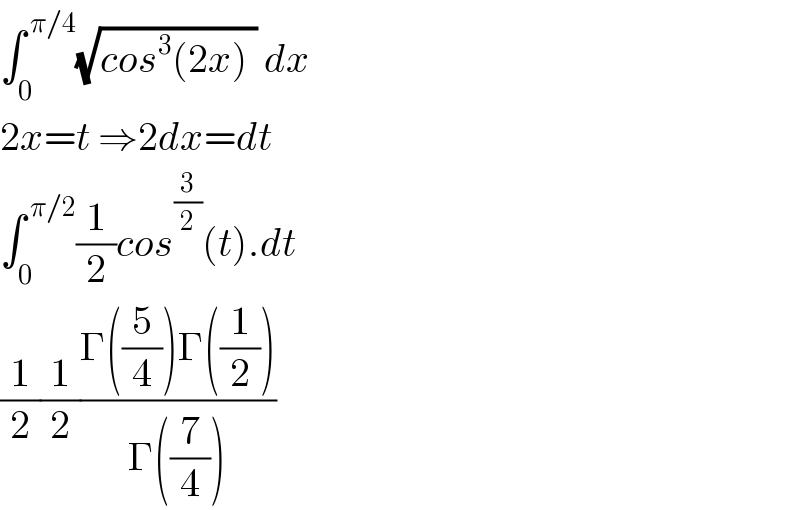
$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \sqrt{{cos}^{\mathrm{3}} \left(\mathrm{2}{x}\right)\:}\:{dx} \\ $$$$\mathrm{2}{x}={t}\:\Rightarrow\mathrm{2}{dx}={dt} \\ $$$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}{cos}^{\frac{\mathrm{3}}{\mathrm{2}}} \left({t}\right).{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{1}}{\mathrm{2}}\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{7}}{\mathrm{4}}\right)} \\ $$
