Question Number 140684 by qaz last updated on 11/May/21

$$\int_{\mathrm{0}} ^{\pi} \mathrm{cos}\:^{{n}} \left({x}\right)\centerdot\mathrm{cos}\:\left({nx}\right){dx}=\frac{\pi}{\mathrm{2}^{{n}} } \\ $$
Answered by mnjuly1970 last updated on 11/May/21
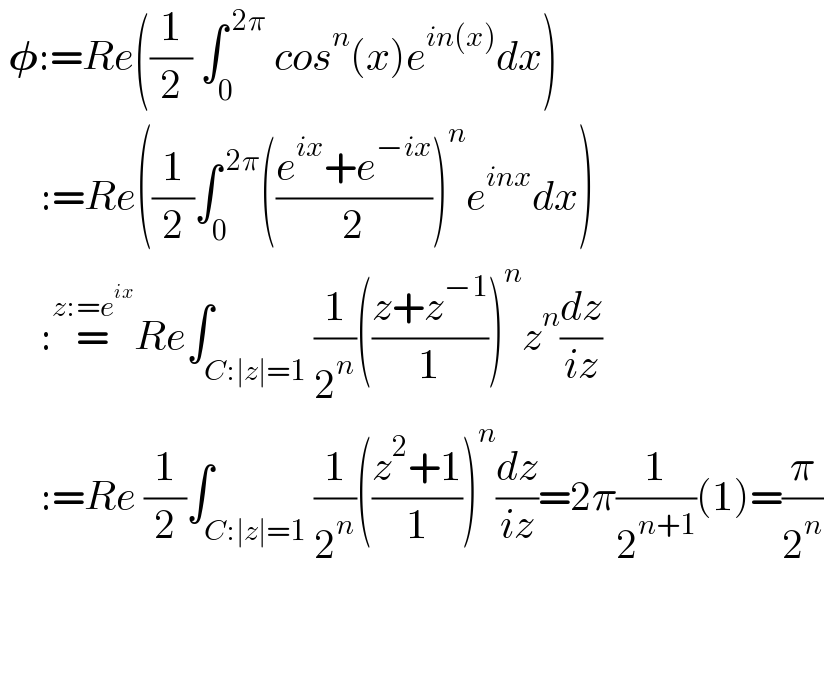
$$\:\boldsymbol{\phi}:={Re}\left(\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} \:{cos}^{{n}} \left({x}\right){e}^{{in}\left({x}\right)} {dx}\right) \\ $$$$\:\:\:\:\::={Re}\left(\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} \left(\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}}\right)^{{n}} {e}^{{inx}} {dx}\right) \\ $$$$\:\:\:\:\::\overset{{z}:={e}^{{ix}} } {=}{Re}\int_{{C}:\mid{z}\mid=\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}^{{n}} }\left(\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{1}}\right)^{{n}} {z}^{{n}} \frac{{dz}}{{iz}} \\ $$$$\:\:\:\:\::={Re}\:\frac{\mathrm{1}}{\mathrm{2}}\int_{{C}:\mid{z}\mid=\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}^{{n}} }\left(\frac{{z}^{\mathrm{2}} +\mathrm{1}}{\mathrm{1}}\right)^{{n}} \frac{{dz}}{{iz}}=\mathrm{2}\pi\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{2}^{{n}} } \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 11/May/21
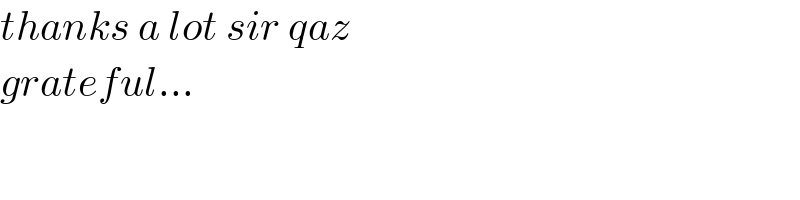
$${thanks}\:{a}\:{lot}\:{sir}\:{qaz} \\ $$$${grateful}… \\ $$
Commented by qaz last updated on 11/May/21
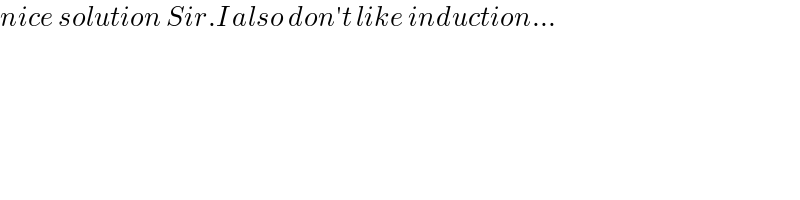
$${nice}\:{solution}\:{Sir}.{I}\:{also}\:{don}'{t}\:{like}\:{induction}… \\ $$
Answered by mathmax by abdo last updated on 11/May/21
![A_n =∫_0 ^π cos^n x .cos(nx)dx ⇒A_n =Re(∫_0 ^π cos^n x e^(inx) dx) but ∫_0 ^π cos^n x e^(inx) dx =∫_0 ^π (((e^(ix) +e^(−ix) )/2))^n e^(inx) dx =(1/2^n ) ∫_0 ^π e^(inx) Σ_(k=0) ^n C_n ^k (e^(ix) )^k (e^(−ix) )^(n−k) dx =(1/2^n )Σ_(k=0) ^n ∫_0 ^π C_n ^k e^(inx) e^(ikx) .e^(−inx) e^(ikx) dx =(1/2^n )Σ_(k=0) ^n C_n ^k ∫_0 ^π e^(2ikx) dx =(π/2^n ) +(1/2^n )Σ_(k=1) ^n C_n ^k [(1/(2ik))e^(2ikx) ]_0 ^π =(π/2^n ) +0 =(π/2^n )](https://www.tinkutara.com/question/Q140705.png)
$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\pi} \:\mathrm{cos}^{\mathrm{n}} \mathrm{x}\:.\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx}\:\Rightarrow\mathrm{A}_{\mathrm{n}} =\mathrm{Re}\left(\int_{\mathrm{0}} ^{\pi} \:\mathrm{cos}^{\mathrm{n}} \mathrm{x}\:\mathrm{e}^{\mathrm{inx}} \:\mathrm{dx}\right)\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\mathrm{cos}^{\mathrm{n}} \mathrm{x}\:\mathrm{e}^{\mathrm{inx}} \:\mathrm{dx}\:=\int_{\mathrm{0}} ^{\pi} \:\left(\frac{\mathrm{e}^{\mathrm{ix}} \:+\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2}}\right)^{\mathrm{n}} \:\mathrm{e}^{\mathrm{inx}} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{\mathrm{inx}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{k}} \:\left(\mathrm{e}^{−\mathrm{ix}} \right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\pi} \mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{inx}} \:\mathrm{e}^{\mathrm{ikx}} \:.\mathrm{e}^{−\mathrm{inx}} \:\mathrm{e}^{\mathrm{ikx}} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{\mathrm{2ikx}} \:\mathrm{dx}\:=\frac{\pi}{\mathrm{2}^{\mathrm{n}} }\:+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left[\frac{\mathrm{1}}{\mathrm{2ik}}\mathrm{e}^{\mathrm{2ikx}} \right]_{\mathrm{0}} ^{\pi} \\ $$$$=\frac{\pi}{\mathrm{2}^{\mathrm{n}} }\:+\mathrm{0}\:=\frac{\pi}{\mathrm{2}^{\mathrm{n}} } \\ $$
