Question Number 137656 by rs4089 last updated on 05/Apr/21
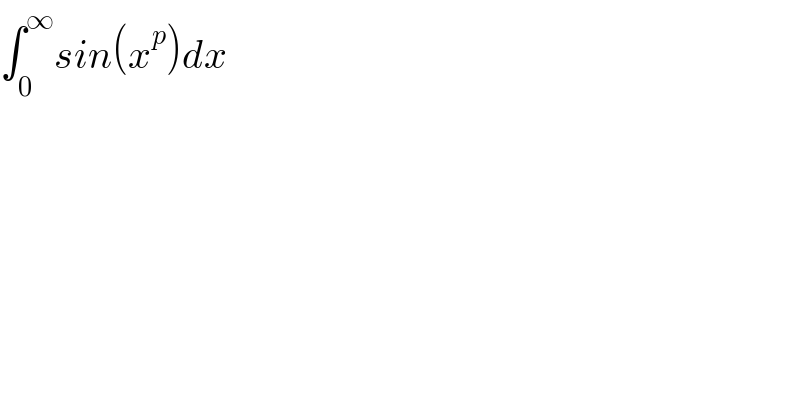
$$\int_{\mathrm{0}} ^{\infty} {sin}\left({x}^{{p}} \right){dx} \\ $$
Answered by Dwaipayan Shikari last updated on 05/Apr/21
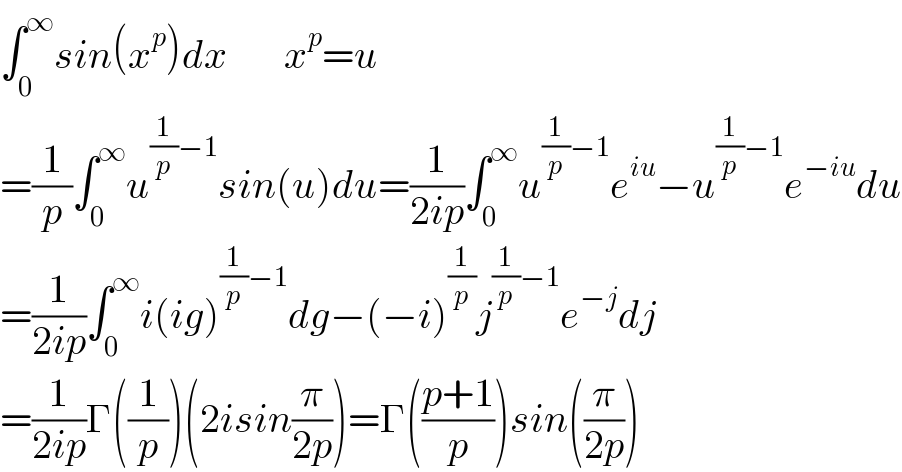
$$\int_{\mathrm{0}} ^{\infty} {sin}\left({x}^{{p}} \right){dx}\:\:\:\:\:\:\:{x}^{{p}} ={u} \\ $$$$=\frac{\mathrm{1}}{{p}}\int_{\mathrm{0}} ^{\infty} {u}^{\frac{\mathrm{1}}{{p}}−\mathrm{1}} {sin}\left({u}\right){du}=\frac{\mathrm{1}}{\mathrm{2}{ip}}\int_{\mathrm{0}} ^{\infty} {u}^{\frac{\mathrm{1}}{{p}}−\mathrm{1}} {e}^{{iu}} −{u}^{\frac{\mathrm{1}}{{p}}−\mathrm{1}} {e}^{−{iu}} {du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{ip}}\int_{\mathrm{0}} ^{\infty} {i}\left({ig}\right)^{\frac{\mathrm{1}}{{p}}−\mathrm{1}} {dg}−\left(−{i}\right)^{\frac{\mathrm{1}}{{p}}} {j}^{\frac{\mathrm{1}}{{p}}−\mathrm{1}} {e}^{−{j}} {dj} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{ip}}\Gamma\left(\frac{\mathrm{1}}{{p}}\right)\left(\mathrm{2}{isin}\frac{\pi}{\mathrm{2}{p}}\right)=\Gamma\left(\frac{{p}+\mathrm{1}}{{p}}\right){sin}\left(\frac{\pi}{\mathrm{2}{p}}\right) \\ $$
