Menu Close

0-u-2-2-u-4-2u-2-2-du-

Tinku Tara 0 Comments
Pin




Question Number 137518 by Lordose last updated on 03/Apr/21
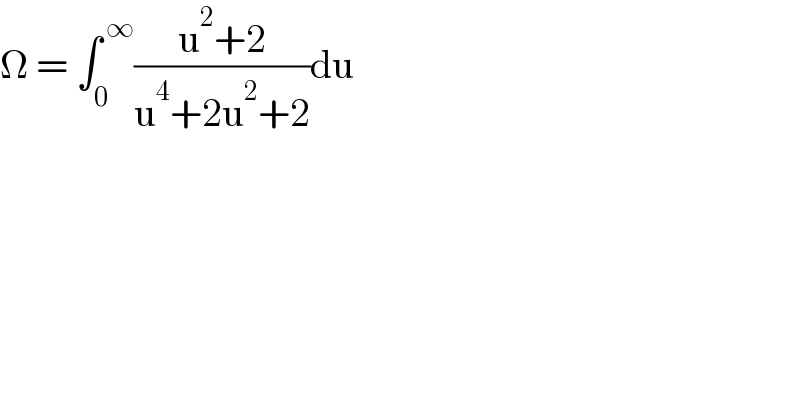
Ω = ∫_0 ^( ∞) ((u^2 +2)/(u^4 +2u^2 +2))du
$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{u}^{\mathrm{2}} +\mathrm{2}}{\mathrm{u}^{\mathrm{4}} +\mathrm{2u}^{\mathrm{2}} +\mathrm{2}}\mathrm{du} \\ $$
Answered by mathmax by abdo last updated on 03/Apr/21
Φ =∫_0 ^∞ ((x^2 +2)/(x^4 +2x^2 +2))dx ⇒Φ =(1/2)∫_(−∞) ^(+∞) ((x^2 +2)/(x^4 +2x^2 +2))dx let ϕ(z)=((z^2 +2)/(z^4 +2z^2 +2)) poles of ϕ? z^4 +2z^2 +2=0 ⇒t^2 +2t+2=0 (t=x^2 ) Δ^′ =1−2=−1 ⇒t_1 =−1+i and t_2 =−1−i t_1 =(√2)(−(1/( (√2)))+(i/( (√2)))) =(√2)e^((i3π)/4) and t_2 =(√2)e^(−((i3π)/4)) ⇒ϕ(z)=((z^2 +2)/((z^2 −(√2)e^((i3π)/4) )(z^2 −(√2)e^(−((i3π)/4)) ))) let α =(√(√2)) ⇒ ϕ(z)=((z^2 +2)/((z−αe^((i3π)/8) )(z+α e^((i3π)/8) )(z−αe^(−((i3π)/8)) )(z+α e^(−i((3π)/8)) ))) ⇒∫_R ϕ(z)dz =2iπ{ Res(ϕ,αe^((i3π)/8) ) +Res(ϕ,−αe^(−((i3π)/8)) )} Res(ϕ,αe^((i3π)/8) ) =((α^2 e^((i3π)/4) +2)/(2αe^((i3π)/8) (√2)(2isin(((3π)/4))))) =((α^2 e^((i3π)/4) +2)/(4iα)) e^(−((i3π)/8)) Res(ϕ ,−α e^(−((i3π)/8)) ) =((α^2 e^(−((3πi)/4)) +2)/(−2α e^(−((i3π)/8)) (−(√2))(2isin(((3π)/4)))) =((α^2 e^(−i((3π)/4)) +2)/(4iα)) e^((i3π)/8) ⇒ ∫_R ϕ(z)dz =2iπ{((α^2 e^((i3π)/4) +2)/(4iα))e^(−((i3π)/8)) +((α^2 e^(−((i3π)/4)) +2)/(4iα)) e^((i3π)/8) } =(π/(2α)){ α^2 e^((i3π)/8) +2e^(−((i3π)/8)) +α^2 e^(−((i3π)/8)) +2e^((i3π)/8) } =(π/(2α)){2α^2 cos(((3π)/8)) +4cos(((3π)/8))} =(π/(2α))(2α^2 +4)cos(((3π)/8)) =(π/α)(α^2 +2)cos(((3π)/8)) =(π/( (√(√2))))((√2)+2)cos(((3π)/8)) =2Φ cos(((3π)/8))=cos((π/8)+(π/4))=cos((π/8))cos((π/4))−sin((π/8))sin((π/4)) =((√(2+(√2)))/2)×(1/( (√2))) −((√(2−(√2)))/2)×(1/( (√2))) and Φ =(π/(2(√(√2))))(2+(√2))cos(((3π)/8))
$$\Phi\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{2x}^{\mathrm{2}} \:+\mathrm{2}}\mathrm{dx}\:\Rightarrow\Phi\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{2x}^{\mathrm{2}} \:+\mathrm{2}}\mathrm{dx}\:\mathrm{let} \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} \:+\mathrm{2}}{\mathrm{z}^{\mathrm{4}} \:+\mathrm{2z}^{\mathrm{2}} \:+\mathrm{2}}\:\:\mathrm{poles}\:\mathrm{of}\:\varphi? \\ $$$$\mathrm{z}^{\mathrm{4}} +\mathrm{2z}^{\mathrm{2}} \:+\mathrm{2}=\mathrm{0}\:\Rightarrow\mathrm{t}^{\mathrm{2}} \:+\mathrm{2t}+\mathrm{2}=\mathrm{0}\:\left(\mathrm{t}=\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\Delta^{'} \:=\mathrm{1}−\mathrm{2}=−\mathrm{1}\:\Rightarrow\mathrm{t}_{\mathrm{1}} =−\mathrm{1}+\mathrm{i}\:\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =−\mathrm{1}−\mathrm{i} \\ $$$$\mathrm{t}_{\mathrm{1}} =\sqrt{\mathrm{2}}\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right)\:=\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{4}}} \:\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =\sqrt{\mathrm{2}}\mathrm{e}^{−\frac{\mathrm{i3}\pi}{\mathrm{4}}} \\ $$$$\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} \:+\mathrm{2}}{\left(\mathrm{z}^{\mathrm{2}} −\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}^{\mathrm{2}} −\sqrt{\mathrm{2}}\mathrm{e}^{−\frac{\mathrm{i3}\pi}{\mathrm{4}}} \right)}\:\:\mathrm{let}\:\:\alpha\:=\sqrt{\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} +\mathrm{2}}{\left(\mathrm{z}−\alpha\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{8}}} \right)\left(\mathrm{z}+\alpha\:\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{8}}} \right)\left(\mathrm{z}−\alpha\mathrm{e}^{−\frac{\mathrm{i3}\pi}{\mathrm{8}}} \right)\left(\mathrm{z}+\alpha\:\mathrm{e}^{−\mathrm{i}\frac{\mathrm{3}\pi}{\mathrm{8}}} \right)} \\ $$$$\Rightarrow\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\:\mathrm{Res}\left(\varphi,\alpha\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{8}}} \right)\:+\mathrm{Res}\left(\varphi,−\alpha\mathrm{e}^{−\frac{\mathrm{i3}\pi}{\mathrm{8}}} \right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\alpha\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{8}}} \right)\:=\frac{\alpha^{\mathrm{2}} \:\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{4}}} \:+\mathrm{2}}{\mathrm{2}\alpha\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{8}}} \:\:\sqrt{\mathrm{2}}\left(\mathrm{2isin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)\right)} \\ $$$$=\frac{\alpha^{\mathrm{2}} \:\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{4}}} \:+\mathrm{2}}{\mathrm{4i}\alpha}\:\mathrm{e}^{−\frac{\mathrm{i3}\pi}{\mathrm{8}}} \\ $$$$\mathrm{Res}\left(\varphi\:,−\alpha\:\mathrm{e}^{−\frac{\mathrm{i3}\pi}{\mathrm{8}}} \right)\:=\frac{\alpha^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{3}\pi\mathrm{i}}{\mathrm{4}}} \:+\mathrm{2}}{−\mathrm{2}\alpha\:\mathrm{e}^{−\frac{\mathrm{i3}\pi}{\mathrm{8}}} \:\left(−\sqrt{\mathrm{2}}\right)\left(\mathrm{2isin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)\right.} \\ $$$$=\frac{\alpha^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \:+\mathrm{2}}{\mathrm{4i}\alpha}\:\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{8}}} \:\Rightarrow \\ $$$$\int_{\mathrm{R}} \:\:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\frac{\alpha^{\mathrm{2}} \:\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{4}}} \:+\mathrm{2}}{\mathrm{4i}\alpha}\mathrm{e}^{−\frac{\mathrm{i3}\pi}{\mathrm{8}}} \:+\frac{\alpha^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{i3}\pi}{\mathrm{4}}} \:+\mathrm{2}}{\mathrm{4i}\alpha}\:\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{8}}} \right\} \\ $$$$=\frac{\pi}{\mathrm{2}\alpha}\left\{\:\:\alpha^{\mathrm{2}} \:\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{8}}} \:+\mathrm{2e}^{−\frac{\mathrm{i3}\pi}{\mathrm{8}}} \:\:\:+\alpha^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{i3}\pi}{\mathrm{8}}} \:+\mathrm{2e}^{\frac{\mathrm{i3}\pi}{\mathrm{8}}} \right\} \\ $$$$=\frac{\pi}{\mathrm{2}\alpha}\left\{\mathrm{2}\alpha^{\mathrm{2}} \:\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:+\mathrm{4cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\right\} \\ $$$$=\frac{\pi}{\mathrm{2}\alpha}\left(\mathrm{2}\alpha^{\mathrm{2}} \:+\mathrm{4}\right)\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:=\frac{\pi}{\alpha}\left(\alpha^{\mathrm{2}} +\mathrm{2}\right)\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$$$=\frac{\pi}{\:\sqrt{\sqrt{\mathrm{2}}}}\left(\sqrt{\mathrm{2}}+\mathrm{2}\right)\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:=\mathrm{2}\Phi \\ $$$$\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)=\mathrm{cos}\left(\frac{\pi}{\mathrm{8}}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{cos}\left(\frac{\pi}{\mathrm{8}}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}\right)−\mathrm{sin}\left(\frac{\pi}{\mathrm{8}}\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right) \\ $$$$=\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:−\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{and}\:\Phi\:=\frac{\pi}{\mathrm{2}\sqrt{\sqrt{\mathrm{2}}}}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *