Question Number 8691 by FilupSmith last updated on 22/Oct/16
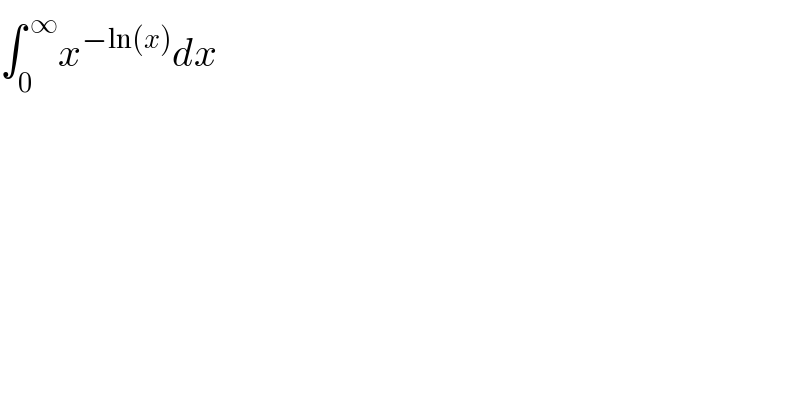
$$\int_{\mathrm{0}} ^{\:\infty} {x}^{−\mathrm{ln}\left({x}\right)} {dx} \\ $$
Commented by FilupSmith last updated on 22/Oct/16

$${x}^{−\mathrm{ln}\left({x}\right)} ={e}^{−\mathrm{ln}\left({x}\right)\mathrm{ln}\left({x}\right)} ={e}^{−\mathrm{ln}^{\mathrm{2}} \left({x}\right)} \\ $$$${u}=\mathrm{ln}\left({x}\right)\:\Rightarrow\:{x}={e}^{{u}} \\ $$$$={e}^{−{u}^{\mathrm{2}} } \\ $$$$\frac{{du}}{{dx}}=\frac{\mathrm{1}}{{x}}\:\Rightarrow\:{dx}={xdu}={e}^{{u}} {du} \\ $$$$\:\: \\ $$$${x}=\mathrm{0}\:\Rightarrow\:{u}=−\infty \\ $$$${x}=\infty\:\Rightarrow\:{u}=\infty \\ $$$$\: \\ $$$$=\int_{−\infty} ^{\:\infty} {e}^{−{u}^{\mathrm{2}} } {e}^{{u}} {du} \\ $$$$=\int_{−\infty} ^{\:\infty} {e}^{{u}−{u}^{\mathrm{2}} } {du} \\ $$$${continue} \\ $$
Answered by prakash jain last updated on 23/Oct/16
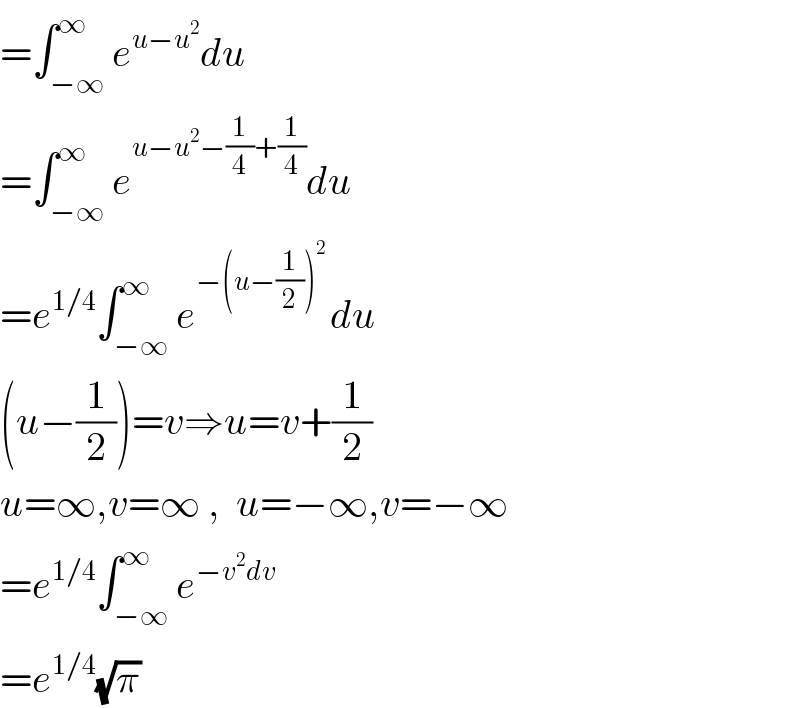
$$=\int_{−\infty} ^{\infty} {e}^{{u}−{u}^{\mathrm{2}} } {du} \\ $$$$=\int_{−\infty} ^{\infty} {e}^{{u}−{u}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}} {du} \\ $$$$={e}^{\mathrm{1}/\mathrm{4}} \int_{−\infty} ^{\infty} {e}^{−\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:} {du} \\ $$$$\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\right)={v}\Rightarrow{u}={v}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${u}=\infty,{v}=\infty\:,\:\:{u}=−\infty,{v}=−\infty \\ $$$$={e}^{\mathrm{1}/\mathrm{4}} \int_{−\infty} ^{\infty} {e}^{−{v}^{\mathrm{2}} {dv}} \\ $$$$={e}^{\mathrm{1}/\mathrm{4}} \sqrt{\pi} \\ $$
