Question Number 143624 by mohammad17 last updated on 16/Jun/21

$$\int_{\mathrm{0}} ^{\:\infty} {z}^{\mathrm{2}} {e}^{\frac{\mathrm{1}}{{z}}} {dz} \\ $$
Answered by Olaf_Thorendsen last updated on 16/Jun/21
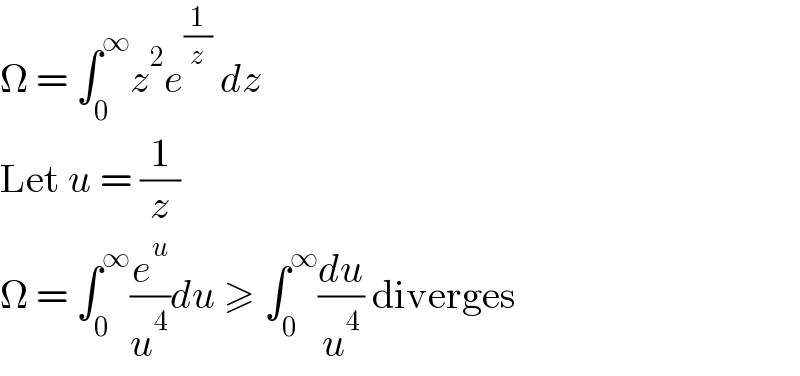
$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} {z}^{\mathrm{2}} {e}^{\frac{\mathrm{1}}{{z}}} \:{dz} \\ $$$$\mathrm{Let}\:{u}\:=\:\frac{\mathrm{1}}{{z}} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{u}} }{{u}^{\mathrm{4}} }{du}\:\geqslant\:\int_{\mathrm{0}} ^{\infty} \frac{{du}}{{u}^{\mathrm{4}} }\:\mathrm{diverges} \\ $$
