Question Number 12144 by rish@bh last updated on 14/Apr/17
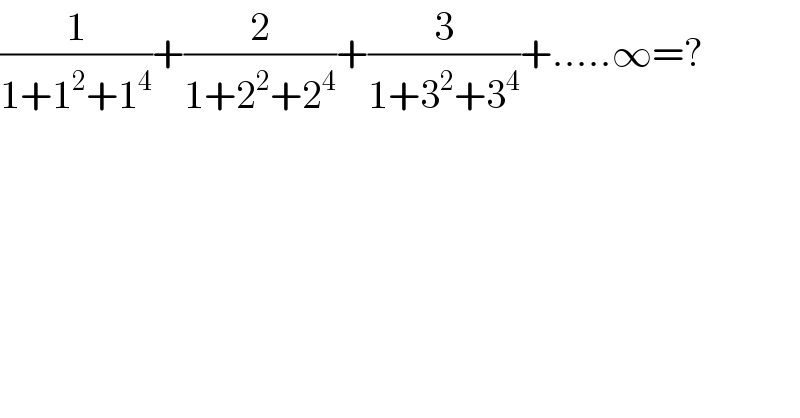
$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{4}} }+\frac{\mathrm{2}}{\mathrm{1}+\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{3}}{\mathrm{1}+\mathrm{3}^{\mathrm{2}} +\mathrm{3}^{\mathrm{4}} }+…..\infty=? \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 14/Apr/17
![(n/(n^4 +n^2 +1))=(n/((n^2 +1)^2 −n^2 ))=(n/((n^2 +n+1)(n^2 −n+1)))= (1/2).(((n^2 +n+1)−(n^2 −n+1))/((n^2 +n+1)(n^2 −n+1)))= (1/2)((1/(n^2 −n+1))−(1/(n^2 +n+1))) LHS=(1/2)[(1/1)−(1/3)+(1/3)−(1/7)+(1/7)−(1/(13)).....−(1/(n^2 +n+1))]= =(1/2).(1−(1/(n^2 +n+1)))=((n^2 +n)/(2(n^2 +n+1))) lim_(x→∝) LHS=(1/2) .■](https://www.tinkutara.com/question/Q12147.png)
$$\frac{{n}}{{n}^{\mathrm{4}} +{n}^{\mathrm{2}} +\mathrm{1}}=\frac{{n}}{\left({n}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −{n}^{\mathrm{2}} }=\frac{{n}}{\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)\left({n}^{\mathrm{2}} −{n}+\mathrm{1}\right)}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}.\frac{\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)−\left({n}^{\mathrm{2}} −{n}+\mathrm{1}\right)}{\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)\left({n}^{\mathrm{2}} −{n}+\mathrm{1}\right)}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{n}+\mathrm{1}}\right) \\ $$$${LHS}=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{13}}…..−\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{n}+\mathrm{1}}\right]= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{n}+\mathrm{1}}\right)=\frac{{n}^{\mathrm{2}} +{n}}{\mathrm{2}\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)} \\ $$$$\underset{{x}\rightarrow\propto} {\mathrm{lim}}{LHS}=\frac{\mathrm{1}}{\mathrm{2}}\:\:.\blacksquare \\ $$
Commented by rish@bh last updated on 14/Apr/17

$$\mathrm{Thanks} \\ $$
