Menu Close

1-1-1-t-dt-

Tinku Tara 0 Comments
Pin




Question Number 142100 by ZiYangLee last updated on 26/May/21
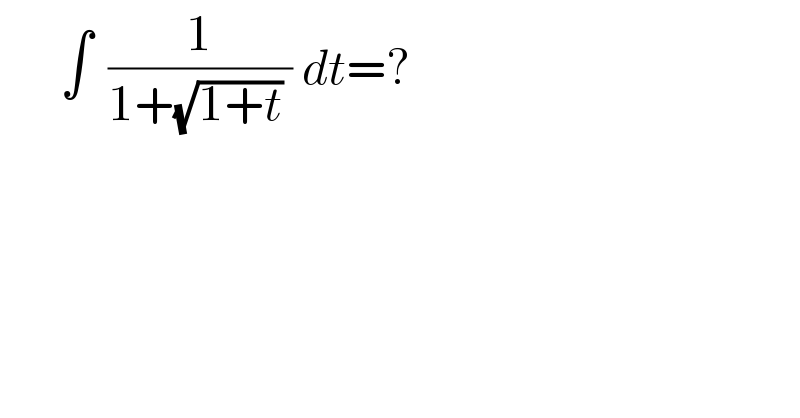
∫^ (1/(1+(√(1+t)) )) dt=?
$$\:\:\:\:\:\:\int^{\:} \:\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{1}+{t}}\:}\:{dt}=? \\ $$
Answered by iloveisrael last updated on 26/May/21
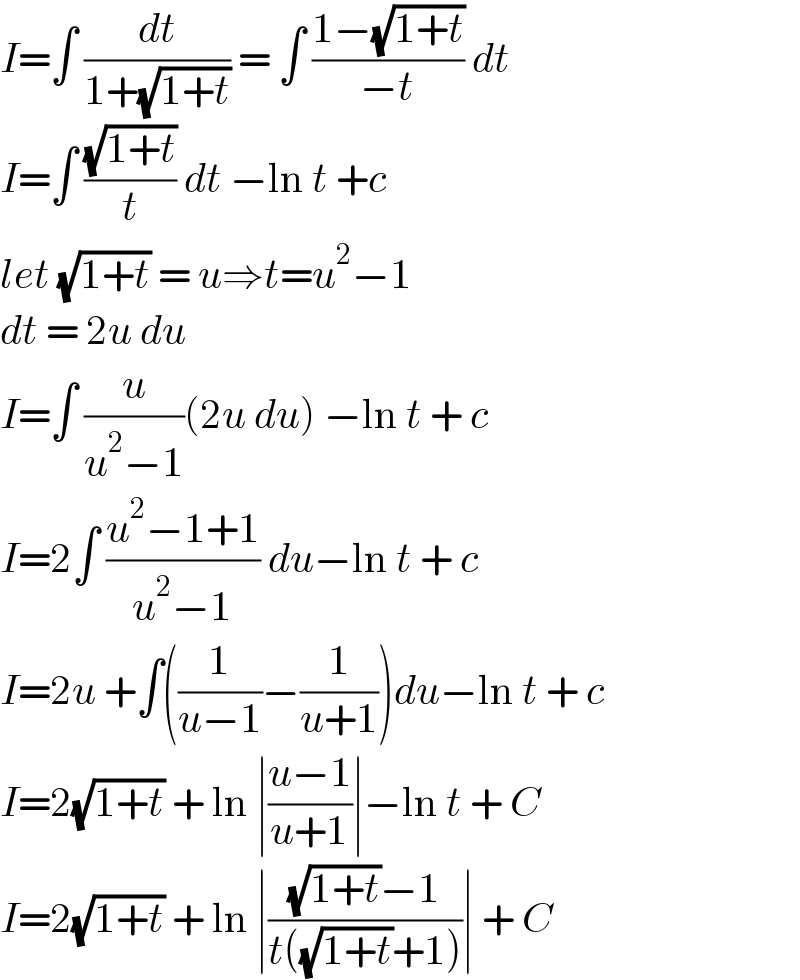
I=∫ (dt/(1+(√(1+t)))) = ∫ ((1−(√(1+t)))/(−t)) dt I=∫ ((√(1+t))/t) dt −ln t +c let (√(1+t)) = u⇒t=u^2 −1 dt = 2u du I=∫ (u/(u^2 −1))(2u du) −ln t + c I=2∫ ((u^2 −1+1)/(u^2 −1)) du−ln t + c I=2u +∫((1/(u−1))−(1/(u+1)))du−ln t + c I=2(√(1+t)) + ln ∣((u−1)/(u+1))∣−ln t + C I=2(√(1+t)) + ln ∣(((√(1+t))−1)/(t((√(1+t))+1)))∣ + C
$${I}=\int\:\frac{{dt}}{\mathrm{1}+\sqrt{\mathrm{1}+{t}}}\:=\:\int\:\frac{\mathrm{1}−\sqrt{\mathrm{1}+{t}}}{−{t}}\:{dt} \\ $$$${I}=\int\:\frac{\sqrt{\mathrm{1}+{t}}}{{t}}\:{dt}\:−\mathrm{ln}\:{t}\:+{c} \\ $$$${let}\:\sqrt{\mathrm{1}+{t}}\:=\:{u}\Rightarrow{t}={u}^{\mathrm{2}} −\mathrm{1} \\ $$$${dt}\:=\:\mathrm{2}{u}\:{du} \\ $$$${I}=\int\:\frac{{u}}{{u}^{\mathrm{2}} −\mathrm{1}}\left(\mathrm{2}{u}\:{du}\right)\:−\mathrm{ln}\:{t}\:+\:{c} \\ $$$${I}=\mathrm{2}\int\:\frac{{u}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{u}^{\mathrm{2}} −\mathrm{1}}\:{du}−\mathrm{ln}\:{t}\:+\:{c} \\ $$$${I}=\mathrm{2}{u}\:+\int\left(\frac{\mathrm{1}}{{u}−\mathrm{1}}−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right){du}−\mathrm{ln}\:{t}\:+\:{c} \\ $$$${I}=\mathrm{2}\sqrt{\mathrm{1}+{t}}\:+\:\mathrm{ln}\:\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid−\mathrm{ln}\:{t}\:+\:{C} \\ $$$${I}=\mathrm{2}\sqrt{\mathrm{1}+{t}}\:+\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{1}+{t}}−\mathrm{1}}{{t}\left(\sqrt{\mathrm{1}+{t}}+\mathrm{1}\right)}\mid\:+\:{C} \\ $$
Answered by mathmax by abdo last updated on 26/May/21
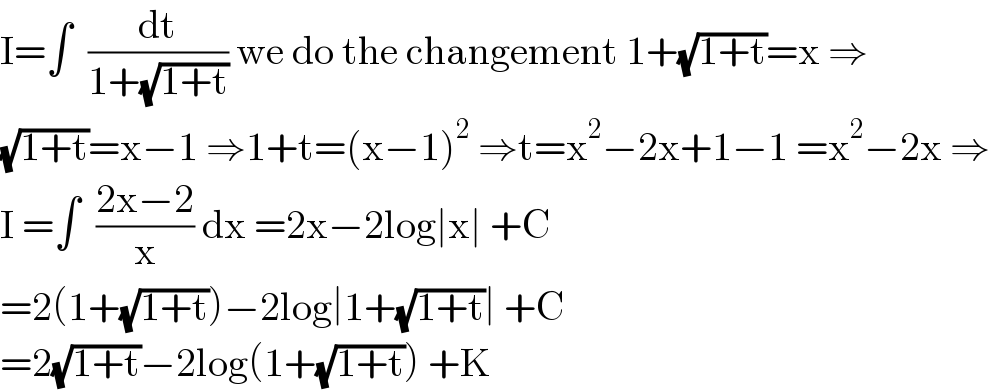
I=∫ (dt/(1+(√(1+t)))) we do the changement 1+(√(1+t))=x ⇒ (√(1+t))=x−1 ⇒1+t=(x−1)^2 ⇒t=x^2 −2x+1−1 =x^2 −2x ⇒ I =∫ ((2x−2)/x) dx =2x−2log∣x∣ +C =2(1+(√(1+t)))−2log∣1+(√(1+t))∣ +C =2(√(1+t))−2log(1+(√(1+t))) +K
$$\mathrm{I}=\int\:\:\frac{\mathrm{dt}}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{t}}}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{t}}=\mathrm{x}\:\Rightarrow \\ $$$$\sqrt{\mathrm{1}+\mathrm{t}}=\mathrm{x}−\mathrm{1}\:\Rightarrow\mathrm{1}+\mathrm{t}=\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow\mathrm{t}=\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}−\mathrm{1}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{2x}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\frac{\mathrm{2x}−\mathrm{2}}{\mathrm{x}}\:\mathrm{dx}\:=\mathrm{2x}−\mathrm{2log}\mid\mathrm{x}\mid\:+\mathrm{C} \\ $$$$=\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{t}}\right)−\mathrm{2log}\mid\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{t}}\mid\:+\mathrm{C} \\ $$$$=\mathrm{2}\sqrt{\mathrm{1}+\mathrm{t}}−\mathrm{2log}\left(\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{t}}\right)\:+\mathrm{K} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *