Question Number 136645 by Dwaipayan Shikari last updated on 24/Mar/21
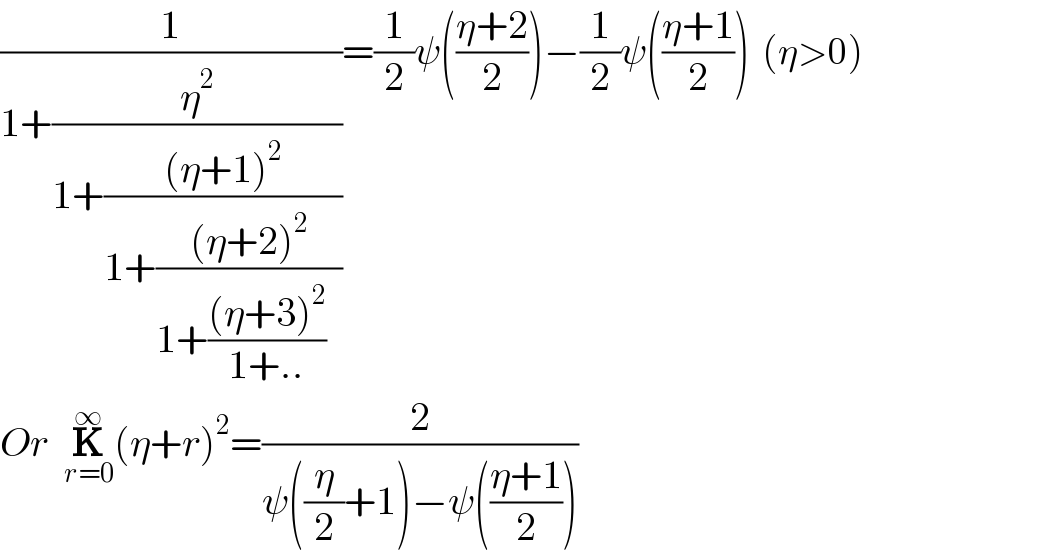
$$\frac{\mathrm{1}}{\mathrm{1}+\frac{\eta^{\mathrm{2}} }{\mathrm{1}+\frac{\left(\eta+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{1}+\frac{\left(\eta+\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{1}+\frac{\left(\eta+\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{1}+..}\:\:}}}}=\frac{\mathrm{1}}{\mathrm{2}}\psi\left(\frac{\eta+\mathrm{2}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\psi\left(\frac{\eta+\mathrm{1}}{\mathrm{2}}\right)\:\:\left(\eta>\mathrm{0}\right) \\ $$$${Or}\:\:\underset{{r}=\mathrm{0}} {\overset{\infty} {\boldsymbol{\mathrm{K}}}}\left(\eta+{r}\right)^{\mathrm{2}} =\frac{\mathrm{2}}{\psi\left(\frac{\eta}{\mathrm{2}}+\mathrm{1}\right)−\psi\left(\frac{\eta+\mathrm{1}}{\mathrm{2}}\right)} \\ $$
