Menu Close

1-1-3-1-2-3-1-5-3-1-10-3-1-17-3-1-26-3-1-37-3-1-50-3-1-65-3-1-82-3-1-101-3-

Tinku Tara 0 Comments
Pin




Question Number 131795 by Dwaipayan Shikari last updated on 08/Feb/21
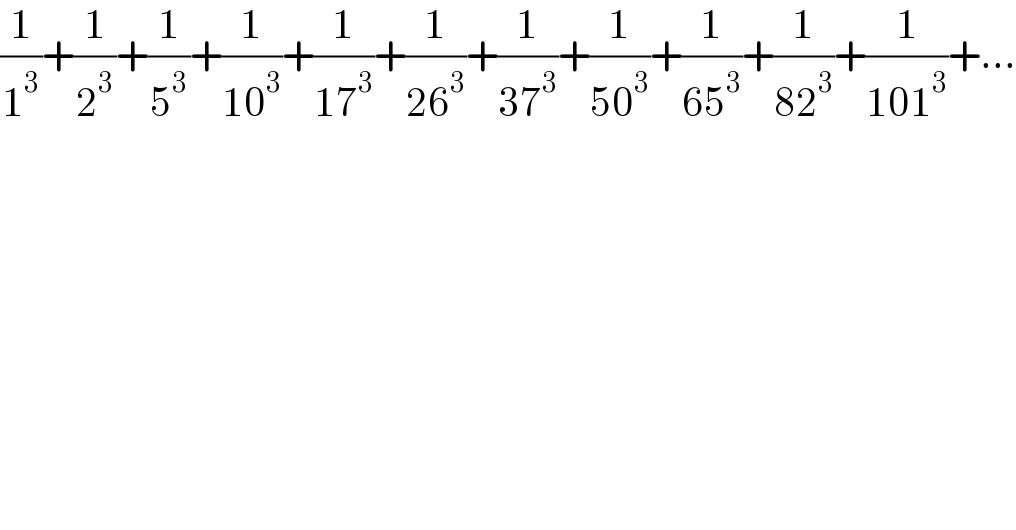
(1/1^3 )+(1/2^3 )+(1/5^3 )+(1/(10^3 ))+(1/(17^3 ))+(1/(26^3 ))+(1/(37^3 ))+(1/(50^3 ))+(1/(65^3 ))+(1/(82^3 ))+(1/(101^3 ))+...
$$\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{10}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{17}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{26}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{37}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{50}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{65}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{82}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{101}^{\mathrm{3}} }+… \\ $$
Answered by Olaf last updated on 08/Feb/21
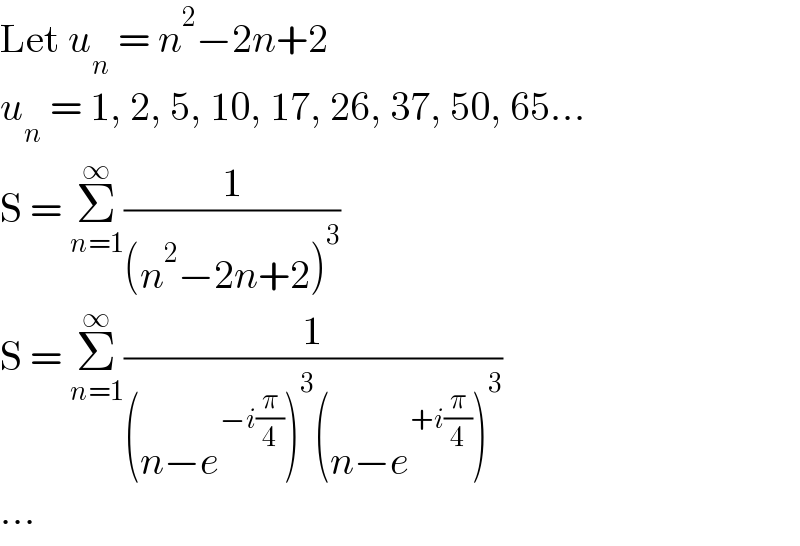
Let u_n = n^2 −2n+2 u_n = 1, 2, 5, 10, 17, 26, 37, 50, 65... S = Σ_(n=1) ^∞ (1/((n^2 −2n+2)^3 )) S = Σ_(n=1) ^∞ (1/((n−e^(−i(π/4)) )^3 (n−e^(+i(π/4)) )^3 )) ...
$$\mathrm{Let}\:{u}_{{n}} \:=\:{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{2} \\ $$$${u}_{{n}} \:=\:\mathrm{1},\:\mathrm{2},\:\mathrm{5},\:\mathrm{10},\:\mathrm{17},\:\mathrm{26},\:\mathrm{37},\:\mathrm{50},\:\mathrm{65}… \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{2}\right)^{\mathrm{3}} } \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}−{e}^{−{i}\frac{\pi}{\mathrm{4}}} \right)^{\mathrm{3}} \left({n}−{e}^{+{i}\frac{\pi}{\mathrm{4}}} \right)^{\mathrm{3}} } \\ $$$$… \\ $$
Commented by mindispower last updated on 08/Feb/21
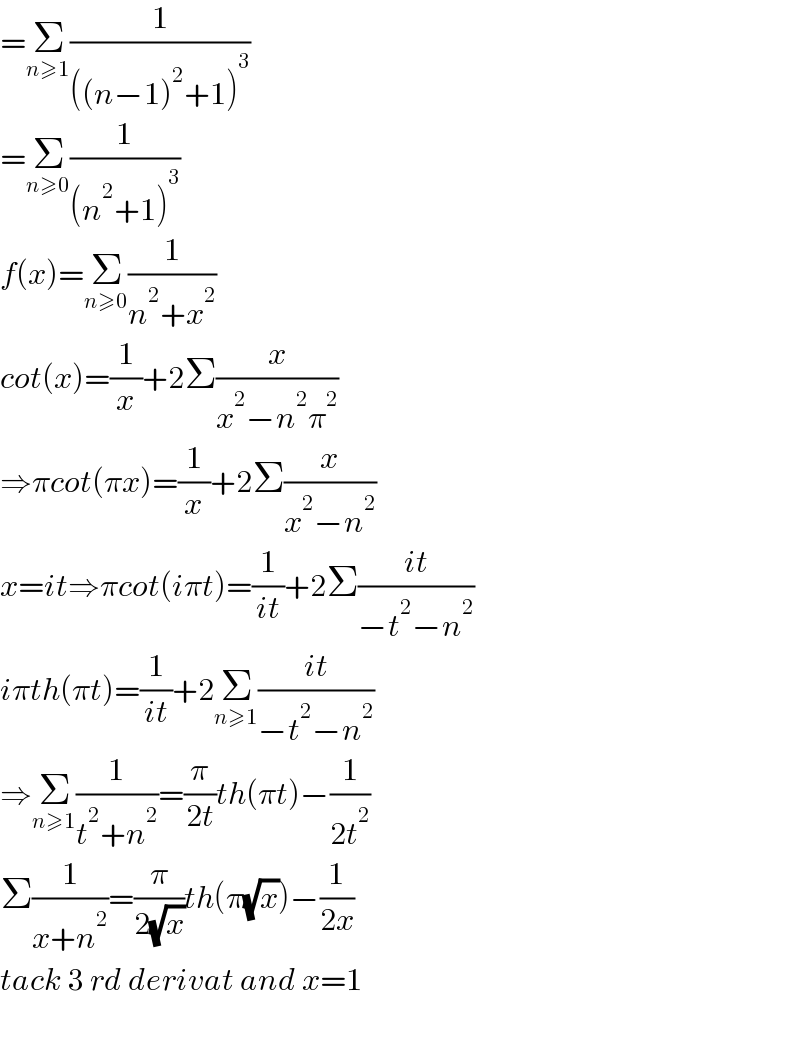
=Σ_(n≥1) (1/(((n−1)^2 +1)^3 )) =Σ_(n≥0) (1/((n^2 +1)^3 )) f(x)=Σ_(n≥0) (1/(n^2 +x^2 )) cot(x)=(1/x)+2Σ(x/(x^2 −n^2 π^2 )) ⇒πcot(πx)=(1/x)+2Σ(x/(x^2 −n^2 )) x=it⇒πcot(iπt)=(1/(it))+2Σ((it)/(−t^2 −n^2 )) iπth(πt)=(1/(it))+2Σ_(n≥1) ((it)/(−t^2 −n^2 )) ⇒Σ_(n≥1) (1/(t^2 +n^2 ))=(π/(2t))th(πt)−(1/(2t^2 )) Σ(1/(x+n^2 ))=(π/(2(√x)))th(π(√x))−(1/(2x)) tack 3 rd derivat and x=1
$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\left({n}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${f}\left({x}\right)=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$${cot}\left({x}\right)=\frac{\mathrm{1}}{{x}}+\mathrm{2}\Sigma\frac{{x}}{{x}^{\mathrm{2}} −{n}^{\mathrm{2}} \pi^{\mathrm{2}} } \\ $$$$\Rightarrow\pi{cot}\left(\pi{x}\right)=\frac{\mathrm{1}}{{x}}+\mathrm{2}\Sigma\frac{{x}}{{x}^{\mathrm{2}} −{n}^{\mathrm{2}} } \\ $$$${x}={it}\Rightarrow\pi{cot}\left({i}\pi{t}\right)=\frac{\mathrm{1}}{{it}}+\mathrm{2}\Sigma\frac{{it}}{−{t}^{\mathrm{2}} −{n}^{\mathrm{2}} } \\ $$$${i}\pi{th}\left(\pi{t}\right)=\frac{\mathrm{1}}{{it}}+\mathrm{2}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{it}}{−{t}^{\mathrm{2}} −{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{t}^{\mathrm{2}} +{n}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}{t}}{th}\left(\pi{t}\right)−\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} } \\ $$$$\Sigma\frac{\mathrm{1}}{{x}+{n}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}\sqrt{{x}}}{th}\left(\pi\sqrt{{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}{x}} \\ $$$${tack}\:\mathrm{3}\:{rd}\:{derivat}\:{and}\:{x}=\mathrm{1} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 08/Feb/21
yes sir!
$${yes}\:{sir}! \\ $$
Commented by mindispower last updated on 09/Feb/21
withe pleasur
$${withe}\:{pleasur} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *