Question Number 137376 by benjo_mathlover last updated on 02/Apr/21
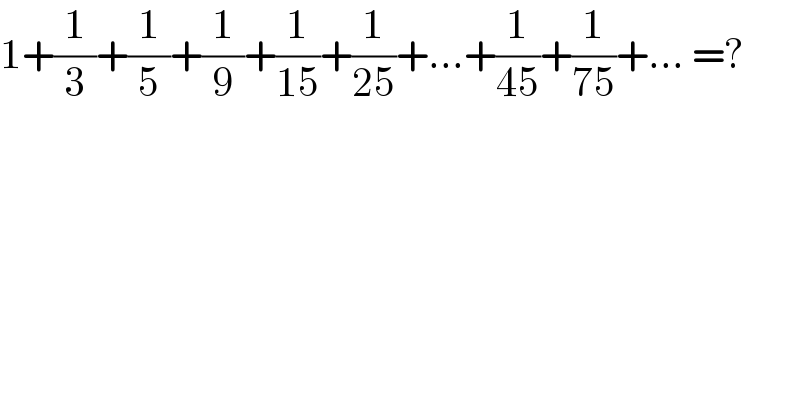
$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{15}}+\frac{\mathrm{1}}{\mathrm{25}}+…+\frac{\mathrm{1}}{\mathrm{45}}+\frac{\mathrm{1}}{\mathrm{75}}+…\:=? \\ $$
Answered by EDWIN88 last updated on 02/Apr/21
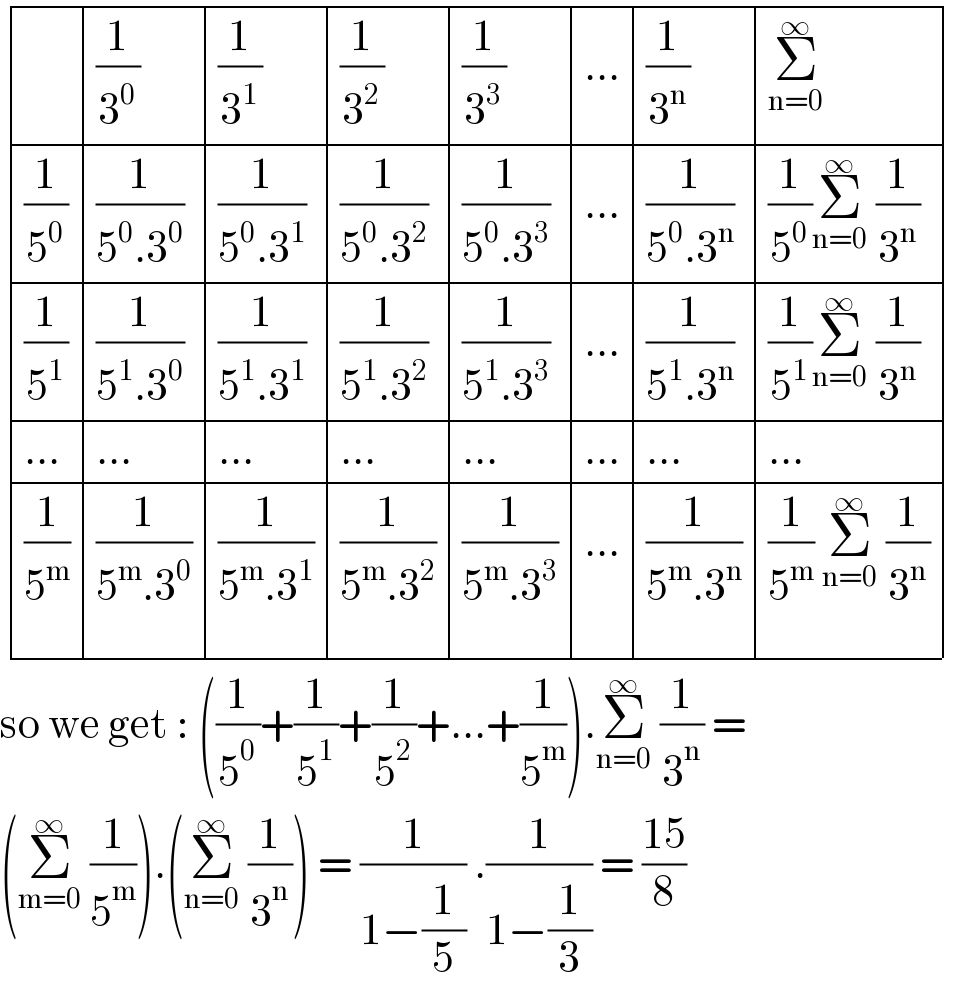
$$\begin{array}{|c|c|c|c|c|}{}&\hline{\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{0}} }}&\hline{\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{1}} }}&\hline{\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }}&\hline{\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }}&\hline{…}&\hline{\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{n}} }}&\hline{\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}}\\{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{0}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{0}} .\mathrm{3}^{\mathrm{0}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{0}} .\mathrm{3}^{\mathrm{1}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{0}} .\mathrm{3}^{\mathrm{2}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{0}} .\mathrm{3}^{\mathrm{3}} }}&\hline{…}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{0}} .\mathrm{3}^{\mathrm{n}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{0}} }\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{n}} }}\\{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{1}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{1}} .\mathrm{3}^{\mathrm{0}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{1}} .\mathrm{3}^{\mathrm{1}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{1}} .\mathrm{3}^{\mathrm{2}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{1}} .\mathrm{3}^{\mathrm{3}} }}&\hline{…}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{1}} .\mathrm{3}^{\mathrm{n}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{1}} }\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{n}} }}\\{…}&\hline{…}&\hline{…}&\hline{…}&\hline{…}&\hline{…}&\hline{…}&\hline{…}\\{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{m}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{m}} .\mathrm{3}^{\mathrm{0}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{m}} .\mathrm{3}^{\mathrm{1}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{m}} .\mathrm{3}^{\mathrm{2}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{m}} .\mathrm{3}^{\mathrm{3}} }}&\hline{…}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{m}} .\mathrm{3}^{\mathrm{n}} }}&\hline{\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{m}} }\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{n}} }}\\\hline\end{array} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{get}\::\:\left(\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{0}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+…+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{m}} }\right).\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{n}} }\:= \\ $$$$\left(\underset{\mathrm{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{m}} }\right).\left(\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{n}} }\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}}\:.\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}\:=\:\frac{\mathrm{15}}{\mathrm{8}} \\ $$
