Question Number 141413 by Willson last updated on 18/May/21
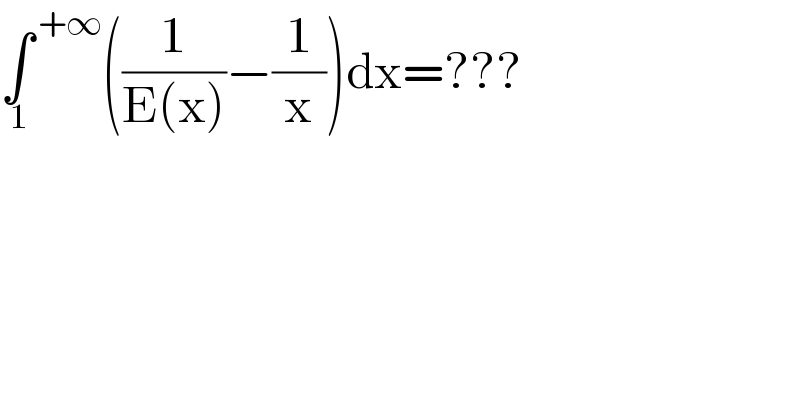
$$\underset{\:\mathrm{1}} {\int}^{\:+\infty} \left(\frac{\mathrm{1}}{\mathrm{E}\left(\mathrm{x}\right)}−\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{dx}=??? \\ $$
Answered by Mathspace last updated on 18/May/21
![=Σ_(n=1) ^(∞ ) ∫_n ^(n+1) ((1/n)−(1/x))dx =Σ_(n=1) ^∞ ((1/n)−[lnx]_n ^(n+1) )dx =Σ_(n=1) ^∞ ((1/n)−ln(n+1)+ln(n)) =Σ_(n=1) ^∞ (1/n) +lim_(n→+∞) Σ_(k=1) ^n lnk−ln(k+1) =H_∞ +lim_(n→+∞) −ln(n+1) =lim_(n→+∞) (H_n −ln(n)−ln(1+(1/n))) =γ](https://www.tinkutara.com/question/Q141429.png)
$$=\sum_{{n}=\mathrm{1}} ^{\infty\:} \int_{{n}} ^{{n}+\mathrm{1}} \left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{{n}}−\left[{lnx}\right]_{{n}} ^{{n}+\mathrm{1}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{{n}}−{ln}\left({n}+\mathrm{1}\right)+{ln}\left({n}\right)\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}}\:+{lim}_{{n}\rightarrow+\infty} \sum_{{k}=\mathrm{1}} ^{{n}} {lnk}−{ln}\left({k}+\mathrm{1}\right) \\ $$$$={H}_{\infty} +{lim}_{{n}\rightarrow+\infty} −{ln}\left({n}+\mathrm{1}\right) \\ $$$$={lim}_{{n}\rightarrow+\infty} \left({H}_{{n}} −{ln}\left({n}\right)−{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\right) \\ $$$$=\gamma \\ $$
