Question Number 143506 by tugu last updated on 15/Jun/21
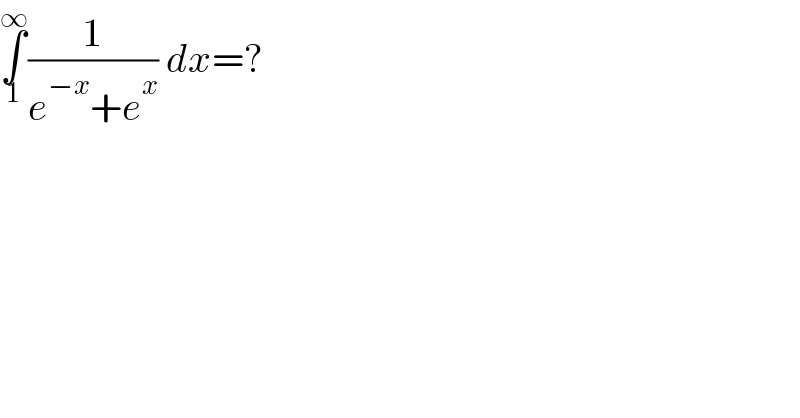
$$\underset{\mathrm{1}} {\overset{\infty} {\int}}\frac{\mathrm{1}}{{e}^{−{x}} +{e}^{{x}} }\:{dx}=? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 15/Jun/21
![∫_1 ^∞ (1/(e^x +e^(−x) ))dx e^x =t =∫_e ^∞ (dt/(t^2 +1)) =[tan^(−1) (t)]_e ^∞ =(π/2)−tan^(−1) (e)=tan^(−1) ((1/e))=0.3525](https://www.tinkutara.com/question/Q143510.png)
$$\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{e}^{{x}} +{e}^{−{x}} }{dx}\:\:\:\:{e}^{{x}} ={t} \\ $$$$=\int_{{e}} ^{\infty} \frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\:=\left[{tan}^{−\mathrm{1}} \left({t}\right)\right]_{{e}} ^{\infty} =\frac{\pi}{\mathrm{2}}−{tan}^{−\mathrm{1}} \left({e}\right)={tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{e}}\right)=\mathrm{0}.\mathrm{3525} \\ $$
