Question Number 221 by 123456 last updated on 25/Jan/15
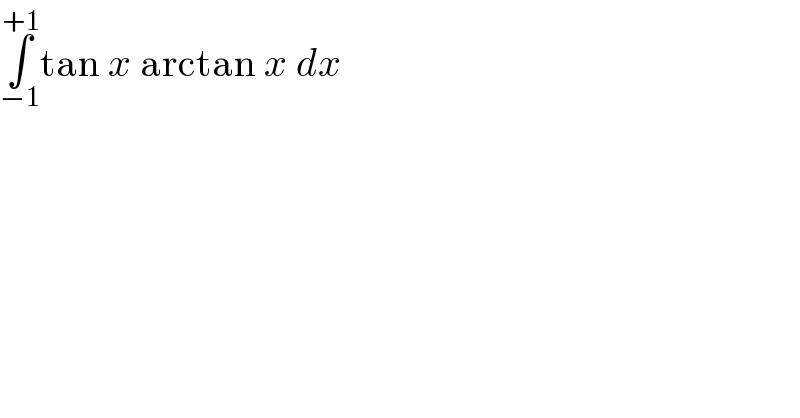
$$\underset{−\mathrm{1}} {\overset{+\mathrm{1}} {\int}}\mathrm{tan}\:{x}\:\mathrm{arctan}\:{x}\:{dx} \\ $$
Answered by mreddy last updated on 16/Dec/14
![∫_(−1) ^(+1) tan x arctan x dx tan x=x+(x^3 /3)+((2x^5 )/(15))+((17x^7 )/(315))+... arctan x=x−(x^3 /3)+(x^5 /5)−(x^7 /7)+... tan x∙arctan x=x^2 +((2x^6 )/9)−((21x^8 )/(315))+... integrating the series [(x^3 /3)+((2x^7 )/(63))−((21x^9 )/(315∙9))+...]_(−1) ^1 ≈0.72](https://www.tinkutara.com/question/Q240.png)
$$\underset{−\mathrm{1}} {\overset{+\mathrm{1}} {\int}}\mathrm{tan}\:{x}\:\mathrm{arctan}\:{x}\:{dx} \\ $$$$\mathrm{tan}\:{x}={x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{15}}+\frac{\mathrm{17}{x}^{\mathrm{7}} }{\mathrm{315}}+… \\ $$$$\mathrm{arctan}\:{x}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−\frac{{x}^{\mathrm{7}} }{\mathrm{7}}+… \\ $$$$\mathrm{tan}\:{x}\centerdot\mathrm{arctan}\:{x}={x}^{\mathrm{2}} +\frac{\mathrm{2}{x}^{\mathrm{6}} }{\mathrm{9}}−\frac{\mathrm{21}{x}^{\mathrm{8}} }{\mathrm{315}}+… \\ $$$$\mathrm{integrating}\:\mathrm{the}\:\mathrm{series} \\ $$$$\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}{x}^{\mathrm{7}} }{\mathrm{63}}−\frac{\mathrm{21}{x}^{\mathrm{9}} }{\mathrm{315}\centerdot\mathrm{9}}+…\right]_{−\mathrm{1}} ^{\mathrm{1}} \approx\mathrm{0}.\mathrm{72} \\ $$
Commented by mreddy last updated on 16/Dec/14

$$\mathrm{Any}\:\mathrm{suggestions}\:\mathrm{for}\:\mathrm{alternative}\:\mathrm{solutions}? \\ $$
