1-2-1-4-1-8-1-2-n-1-1-2-n-P-r-o-v-e-the-above-for-integral-n-1-

Question Number 5723 by Rasheed Soomro last updated on 25/May/16

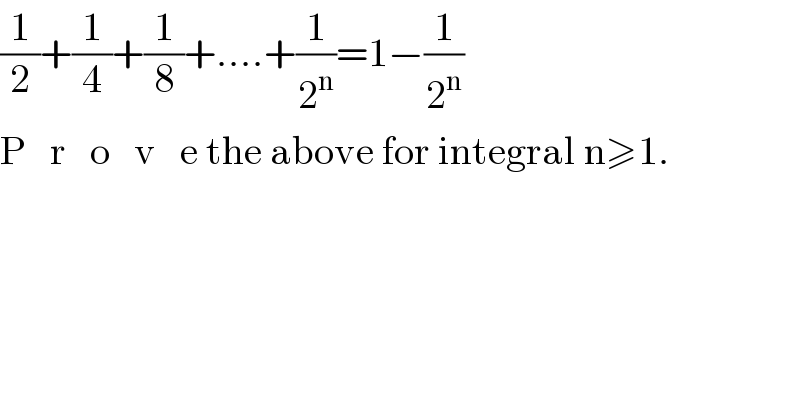
$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}+….+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} } \\ $$$$\mathrm{P}\:\:\:\mathrm{r}\:\:\:\mathrm{o}\:\:\:\mathrm{v}\:\:\:\mathrm{e}\:\mathrm{the}\:\mathrm{above}\:\mathrm{for}\:\mathrm{integral}\:\mathrm{n}\geqslant\mathrm{1}. \\ $$

Commented by FilupSmith last updated on 25/May/16

$$\boldsymbol{\mathrm{LHS}}={S}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}+…+\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$$\mathrm{2}{S}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} } \\ $$$$\mathrm{2}{S}+\frac{\mathrm{1}}{\mathrm{2}^{{n}} }=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$$\mathrm{2}{S}+\frac{\mathrm{1}}{\mathrm{2}^{{n}} }=\mathrm{1}+{S} \\ $$$$\therefore\:{S}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$$\therefore\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{\mathrm{2}^{{n}} }=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare \\ $$

Commented by Rasheed Soomro last updated on 25/May/16

$$\mathcal{G}{oo}\mathcal{D}\:\mathcal{A}{pproach}! \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com