Menu Close

1-2-1-4-3-1-9-4-1-16-5-1-25-6-1-36-7-1-49-8-1-64-exp-2-2-pi-2-12-log-2-

Tinku Tara 0 Comments
Pin




Question Number 142035 by Dwaipayan Shikari last updated on 25/May/21
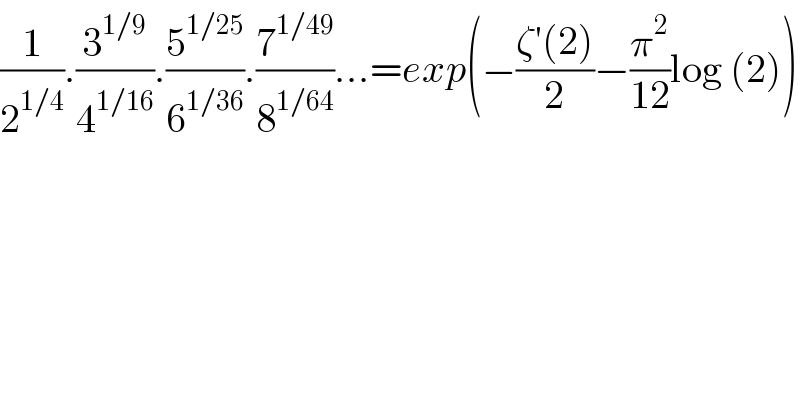
(1/2^(1/4) ).(3^(1/9) /4^(1/16) ).(5^(1/25) /6^(1/36) ).(7^(1/49) /8^(1/64) )...=exp(−((ζ′(2))/2)−(π^2 /(12))log (2))
$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}/\mathrm{4}} }.\frac{\mathrm{3}^{\mathrm{1}/\mathrm{9}} }{\mathrm{4}^{\mathrm{1}/\mathrm{16}} }.\frac{\mathrm{5}^{\mathrm{1}/\mathrm{25}} }{\mathrm{6}^{\mathrm{1}/\mathrm{36}} }.\frac{\mathrm{7}^{\mathrm{1}/\mathrm{49}} }{\mathrm{8}^{\mathrm{1}/\mathrm{64}} }…={exp}\left(−\frac{\zeta'\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\mathrm{log}\:\left(\mathrm{2}\right)\right) \\ $$
Answered by mindispower last updated on 25/May/21
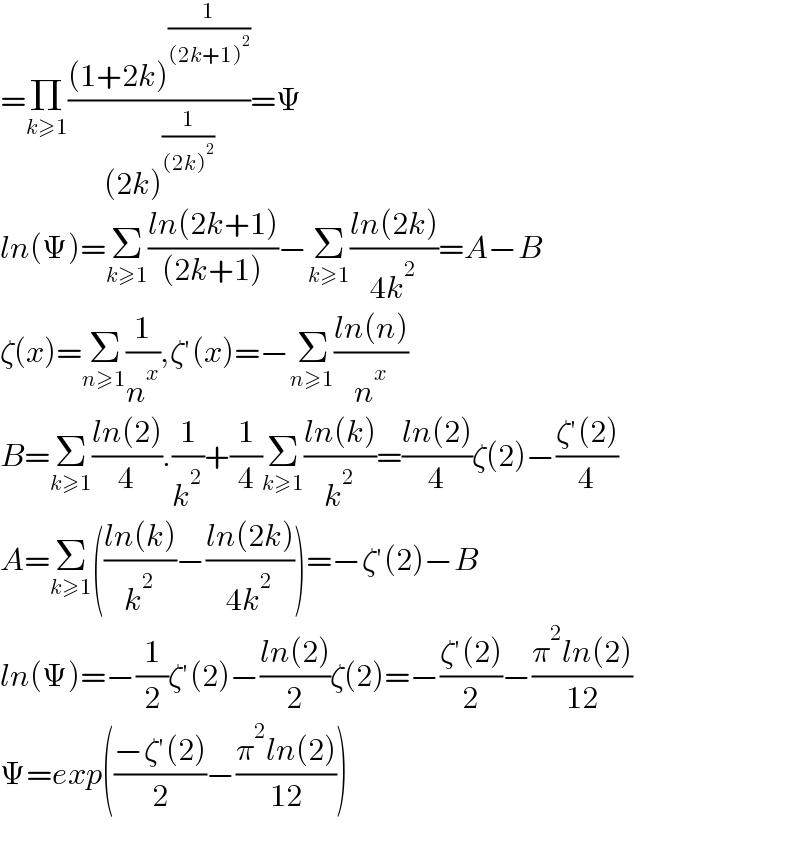
=Π_(k≥1) (((1+2k)^(1/((2k+1)^2 )) )/((2k)^(1/((2k)^2 )) ))=Ψ ln(Ψ)=Σ_(k≥1) ((ln(2k+1))/((2k+1)))−Σ_(k≥1) ((ln(2k))/(4k^2 ))=A−B ζ(x)=Σ_(n≥1) (1/n^x ),ζ′(x)=−Σ_(n≥1) ((ln(n))/n^x ) B=Σ_(k≥1) ((ln(2))/4).(1/k^2 )+(1/4)Σ_(k≥1) ((ln(k))/k^2 )=((ln(2))/4)ζ(2)−((ζ′(2))/4) A=Σ_(k≥1) (((ln(k))/k^2 )−((ln(2k))/(4k^2 )))=−ζ′(2)−B ln(Ψ)=−(1/2)ζ′(2)−((ln(2))/2)ζ(2)=−((ζ′(2))/2)−((π^2 ln(2))/(12)) Ψ=exp(((−ζ′(2))/2)−((π^2 ln(2))/(12)))
$$=\underset{{k}\geqslant\mathrm{1}} {\prod}\frac{\left(\mathrm{1}+\mathrm{2}{k}\right)^{\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }} }{\left(\mathrm{2}{k}\right)^{\frac{\mathrm{1}}{\left(\mathrm{2}{k}\right)^{\mathrm{2}} }} }=\Psi \\ $$$${ln}\left(\Psi\right)=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{ln}\left(\mathrm{2}{k}+\mathrm{1}\right)}{\left(\mathrm{2}{k}+\mathrm{1}\right)}−\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{ln}\left(\mathrm{2}{k}\right)}{\mathrm{4}{k}^{\mathrm{2}} }={A}−{B} \\ $$$$\zeta\left({x}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{{x}} },\zeta'\left({x}\right)=−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{ln}\left({n}\right)}{{n}^{{x}} } \\ $$$${B}=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{4}}.\frac{\mathrm{1}}{{k}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{ln}\left({k}\right)}{{k}^{\mathrm{2}} }=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\zeta\left(\mathrm{2}\right)−\frac{\zeta'\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$${A}=\underset{{k}\geqslant\mathrm{1}} {\sum}\left(\frac{{ln}\left({k}\right)}{{k}^{\mathrm{2}} }−\frac{{ln}\left(\mathrm{2}{k}\right)}{\mathrm{4}{k}^{\mathrm{2}} }\right)=−\zeta'\left(\mathrm{2}\right)−{B} \\ $$$${ln}\left(\Psi\right)=−\frac{\mathrm{1}}{\mathrm{2}}\zeta'\left(\mathrm{2}\right)−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\zeta\left(\mathrm{2}\right)=−\frac{\zeta'\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{12}} \\ $$$$\Psi={exp}\left(\frac{−\zeta'\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{12}}\right) \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 25/May/21
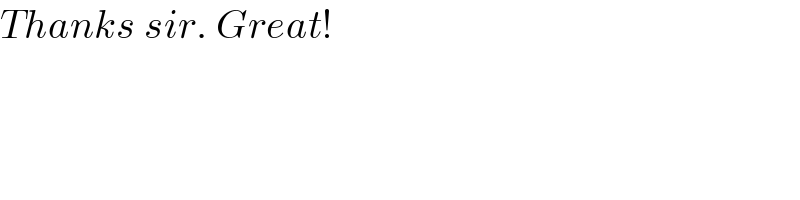
Thanks sir. Great!
$${Thanks}\:{sir}.\:{Great}! \\ $$
Commented by mindispower last updated on 26/May/21
pleasur sir
$${pleasur}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *