Question Number 10493 by ABD last updated on 14/Feb/17
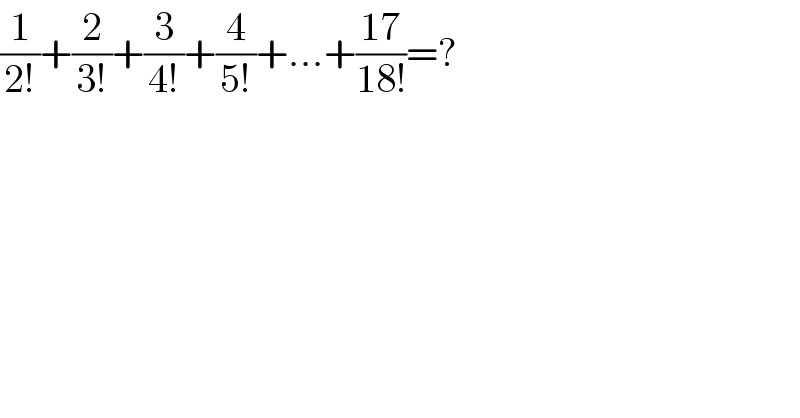
$$\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{2}}{\mathrm{3}!}+\frac{\mathrm{3}}{\mathrm{4}!}+\frac{\mathrm{4}}{\mathrm{5}!}+…+\frac{\mathrm{17}}{\mathrm{18}!}=? \\ $$
Answered by mrW1 last updated on 14/Feb/17
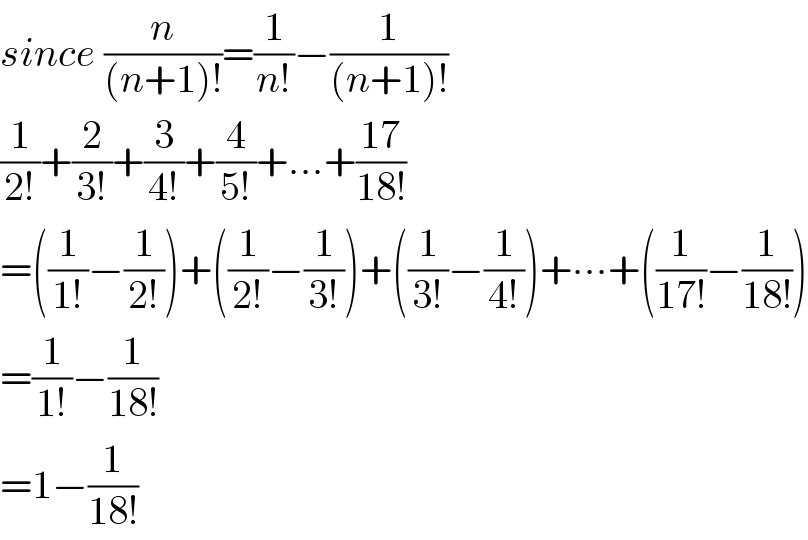
$${since}\:\frac{{n}}{\left({n}+\mathrm{1}\right)!}=\frac{\mathrm{1}}{{n}!}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{2}}{\mathrm{3}!}+\frac{\mathrm{3}}{\mathrm{4}!}+\frac{\mathrm{4}}{\mathrm{5}!}+…+\frac{\mathrm{17}}{\mathrm{18}!} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{1}!}−\frac{\mathrm{1}}{\mathrm{2}!}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}!}−\frac{\mathrm{1}}{\mathrm{4}!}\right)+\centerdot\centerdot\centerdot+\left(\frac{\mathrm{1}}{\mathrm{17}!}−\frac{\mathrm{1}}{\mathrm{18}!}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}!}−\frac{\mathrm{1}}{\mathrm{18}!} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{18}!} \\ $$
Answered by robocop last updated on 14/Feb/17
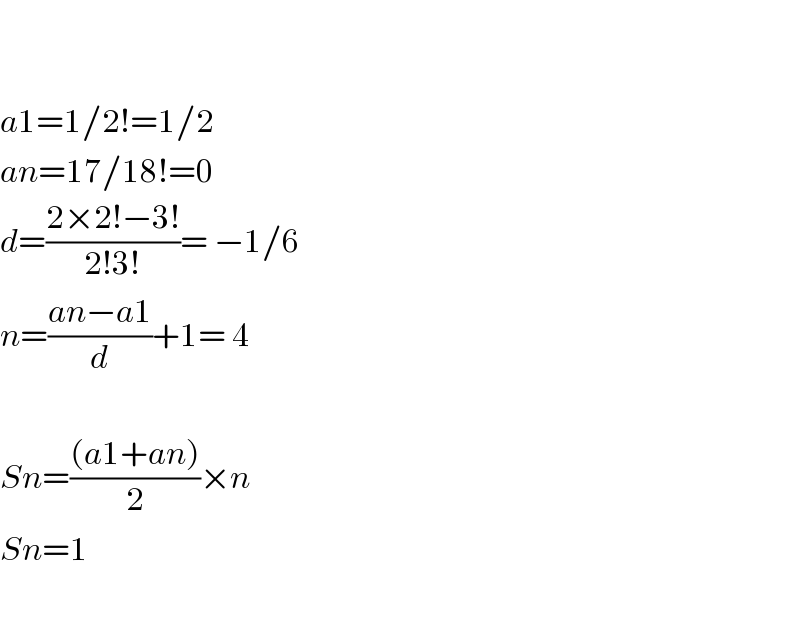
$$ \\ $$$$ \\ $$$${a}\mathrm{1}=\mathrm{1}/\mathrm{2}!=\mathrm{1}/\mathrm{2} \\ $$$${an}=\mathrm{17}/\mathrm{18}!=\mathrm{0} \\ $$$${d}=\frac{\mathrm{2}×\mathrm{2}!−\mathrm{3}!}{\mathrm{2}!\mathrm{3}!}=\:−\mathrm{1}/\mathrm{6} \\ $$$${n}=\frac{{an}−{a}\mathrm{1}}{{d}}+\mathrm{1}=\:\mathrm{4} \\ $$$$ \\ $$$${Sn}=\frac{\left({a}\mathrm{1}+{an}\right)}{\mathrm{2}}×{n} \\ $$$${Sn}=\mathrm{1} \\ $$$$ \\ $$
Commented by FilupS last updated on 15/Feb/17

$$\mathrm{this}\:\mathrm{method}\:\mathrm{wont}\:\mathrm{work}\:\mathrm{because}\:\mathrm{a}\:\mathrm{sequence} \\ $$$$\mathrm{of}\:\mathrm{factorials}\:\mathrm{is}\:\mathrm{product}\:\mathrm{based}\:\mathrm{and}\:\mathrm{they} \\ $$$$\mathrm{grow}\:\mathrm{exponentially}\:\mathrm{larger}.\:\mathrm{i}.\mathrm{e}. \\ $$$$ \\ $$$$\mathrm{let}\:{S}={n}!+\left({n}+\mathrm{1}\right)!+\left({n}+\mathrm{2}\right)!+… \\ $$$$\mathrm{if}\:{d}={t}_{\mathrm{2}} −{t}_{\mathrm{1}} ={t}_{\mathrm{3}} −{t}_{\mathrm{2}} \\ $$$$\therefore\:{d}=\left({n}+\mathrm{1}\right)!−{n}!=\left({n}+\mathrm{2}\right)!−\left({n}+\mathrm{1}\right)! \\ $$$$\:\:\:\:\:\:\:={n}!\centerdot\left(\left({n}+\mathrm{1}\right)−\mathrm{1}\right)=\left({n}+\mathrm{1}\right)!\centerdot\left(\left({n}+\mathrm{2}\right)−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:={n}!\centerdot\left({n}\right)=\left({n}+\mathrm{1}\right)!\centerdot\left({n}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:={n}!\centerdot\left({n}\right)=\left({n}\right)!\centerdot\left({n}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{clear}\:\mathrm{contradiction},\:\mathrm{because}\:\mathrm{the} \\ $$$$\mathrm{RHS}\:\mathrm{is}\:\mathrm{larger}\:\mathrm{by}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{of}\:\:\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{{n}},\: \\ $$$$\mathrm{rather}\:\mathrm{than}\:\mathrm{being}\:\mathrm{larger}\:\mathrm{than}\:\mathrm{a}\:\mathrm{common} \\ $$$$\mathrm{difference}. \\ $$
Commented by robocop last updated on 15/Feb/17

$$ \\ $$$$ \\ $$$$ \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{18}!}=\frac{\mathrm{18}!−\mathrm{1}}{\mathrm{18}!}=\mathrm{1} \\ $$
Commented by FilupS last updated on 16/Feb/17
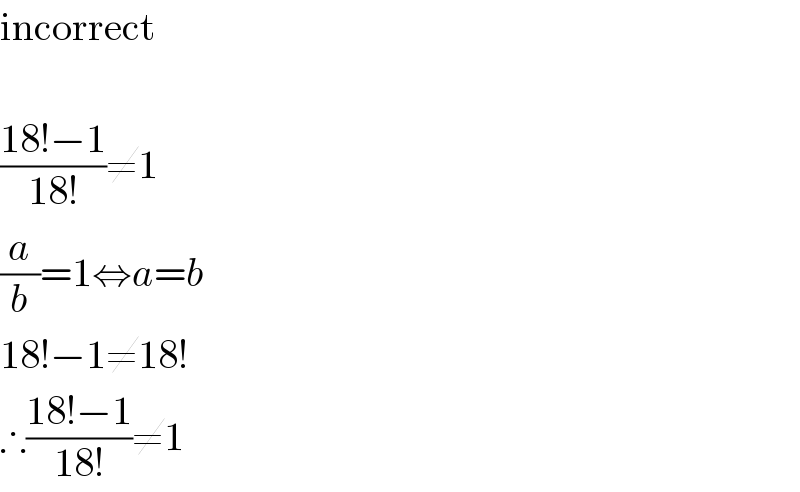
$$\mathrm{incorrect} \\ $$$$\: \\ $$$$\frac{\mathrm{18}!−\mathrm{1}}{\mathrm{18}!}\neq\mathrm{1} \\ $$$$\frac{{a}}{{b}}=\mathrm{1}\Leftrightarrow{a}={b} \\ $$$$\mathrm{18}!−\mathrm{1}\neq\mathrm{18}! \\ $$$$\therefore\frac{\mathrm{18}!−\mathrm{1}}{\mathrm{18}!}\neq\mathrm{1} \\ $$
