Question Number 136489 by liberty last updated on 22/Mar/21
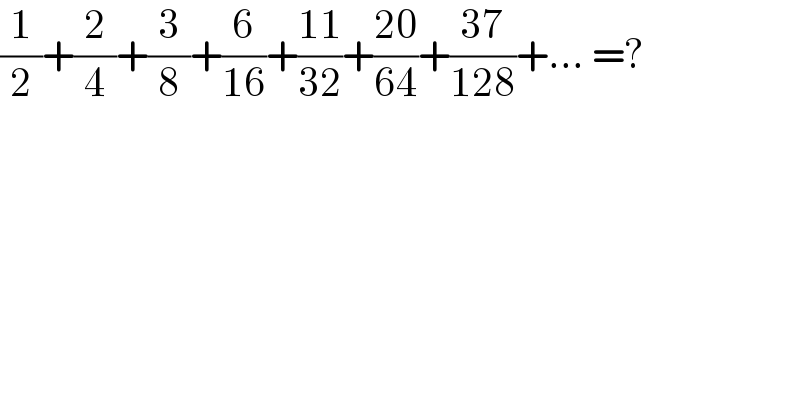
$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{8}}+\frac{\mathrm{6}}{\mathrm{16}}+\frac{\mathrm{11}}{\mathrm{32}}+\frac{\mathrm{20}}{\mathrm{64}}+\frac{\mathrm{37}}{\mathrm{128}}+…\:=? \\ $$
Answered by Olaf last updated on 22/Mar/21

$$\mathrm{Tribonacci}\:\mathrm{numbers}\:: \\ $$$$\mathrm{T}_{\mathrm{0}} \:=\:\mathrm{0},\:\mathrm{T}_{\mathrm{1}} \:=\:\mathrm{1},\:\mathrm{T}_{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\mathrm{T}_{{n}} \:=\:\mathrm{T}_{{n}−\mathrm{1}} +\mathrm{T}_{{n}−\mathrm{2}} +\mathrm{T}_{{n}−\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{T}_{{n}} \:=\:\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{6},\:\mathrm{11},\:\mathrm{20},\:\mathrm{37}…\right\} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{\mathrm{T}_{{n}} }{\mathrm{2}^{{n}−\mathrm{2}} }\:=\:\mathrm{4}\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{\mathrm{T}_{{n}} }{\mathrm{2}^{{n}} }\:=\:\mathrm{4}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{T}_{{n}} }{\mathrm{2}^{{n}} }−\mathrm{2} \\ $$$$\mathrm{The}\:\mathrm{generator}\:\mathrm{function}\:\mathrm{of}\:\left\{\mathrm{T}_{{n}} \right\}\:\mathrm{is} \\ $$$$\mathrm{given}\:\mathrm{by}\:: \\ $$$$\mathrm{F}\left(\mathrm{X}\right)\:=\:\frac{\mathrm{X}−\mathrm{X}^{\mathrm{2}} }{\mathrm{1}−\mathrm{X}−\mathrm{X}^{\mathrm{2}} −\mathrm{X}^{\mathrm{3}} }\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{T}_{{n}} \mathrm{X}^{{n}} \\ $$$$\Rightarrow\:\mathrm{S}\:=\:\mathrm{4F}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2} \\ $$$$\mathrm{S}\:=\:\mathrm{4}\frac{\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}}}−\mathrm{2}\:=\:\mathrm{6} \\ $$
Commented by Olaf last updated on 22/Mar/21
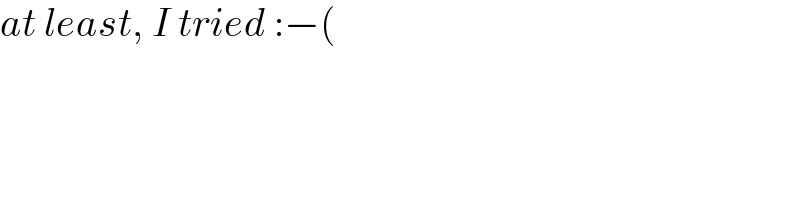
$${at}\:{least},\:{I}\:{tried}\::−\left(\right. \\ $$
Commented by liberty last updated on 23/Mar/21
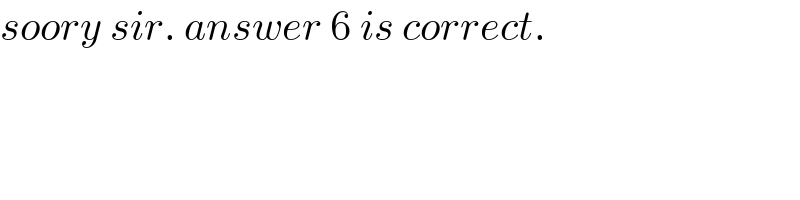
$${soory}\:{sir}.\:{answer}\:\mathrm{6}\:{is}\:{correct}. \\ $$
Commented by liberty last updated on 23/Mar/21

$${thanks}\:{much} \\ $$
