Menu Close

1-2-3-4-5-6-7-8-x-1-2-1-4-1-6-1-8-y-i-0-2i-1-2-i-converge-

Tinku Tara
Pin




Question Number 396 by 123456 last updated on 25/Jan/15
(1/2)−(3/4)+(5/6)−(7/8)+∙∙∙=x (1/2)−(1/4)+(1/6)−(1/8)+...=y −−−−−−−−−−−−−−−−−− Σ_(i=0) ^∞ ((2i+1)/2^i ) converge?
$$\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{6}}−\frac{\mathrm{7}}{\mathrm{8}}+\centerdot\centerdot\centerdot={x} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{8}}+…={y} \\ $$$$−−−−−−−−−−−−−−−−−− \\ $$$$\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{i}+\mathrm{1}}{\mathrm{2}^{{i}} }\:\mathrm{converge}? \\ $$
Commented by 123456 last updated on 28/Dec/14
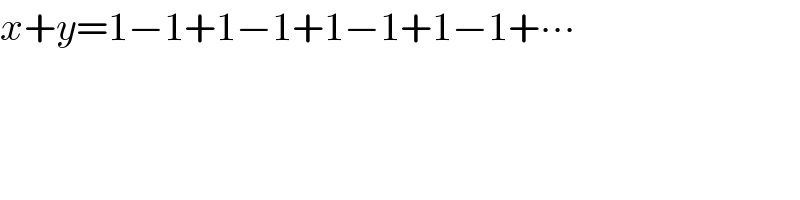
x+y=1−1+1−1+1−1+1−1+∙∙∙
$${x}+{y}=\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+\centerdot\centerdot\centerdot \\ $$
Answered by prakash jain last updated on 29/Dec/14
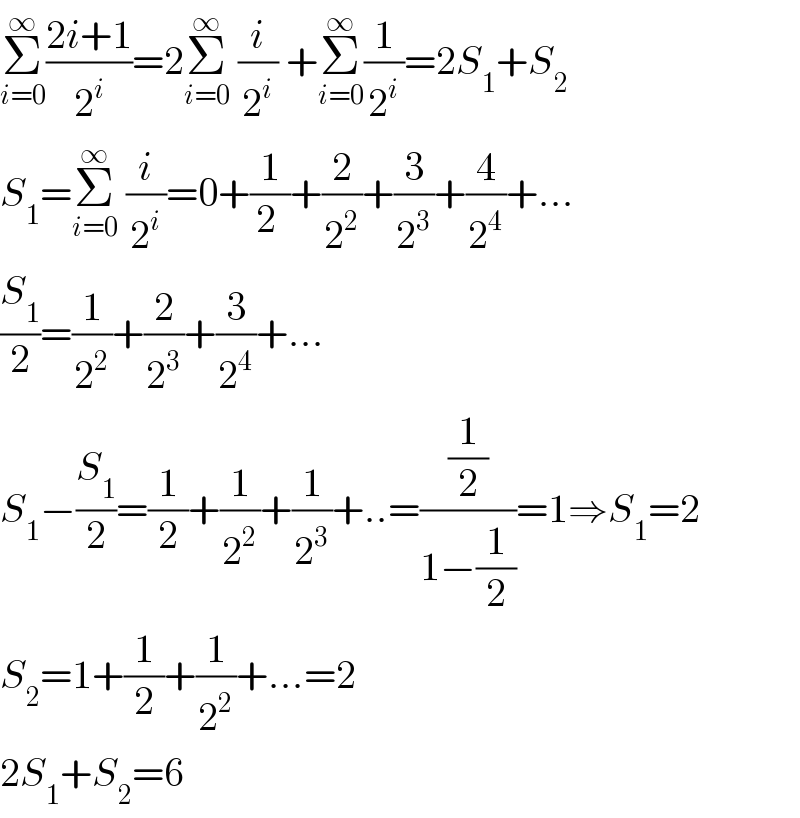
Σ_(i=0) ^∞ ((2i+1)/2^i )=2Σ_(i=0) ^∞ (i/2^i ) +Σ_(i=0) ^∞ (1/2^i )=2S_1 +S_2 S_1 =Σ_(i=0) ^∞ (i/2^i )=0+(1/(2 ))+(2/2^2 )+(3/2^3 )+(4/2^4 )+... (S_1 /2)=(1/2^2 )+(2/2^3 )+(3/2^4 )+... S_1 −(S_1 /2)=(1/2)+(1/2^2 )+(1/2^3 )+..=((1/2)/(1−(1/2)))=1⇒S_1 =2 S_2 =1+(1/2)+(1/2^2 )+...=2 2S_1 +S_2 =6
$$\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{i}+\mathrm{1}}{\mathrm{2}^{{i}} }=\mathrm{2}\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{i}}{\mathrm{2}^{{i}} }\:+\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{i}} }=\mathrm{2}{S}_{\mathrm{1}} +{S}_{\mathrm{2}} \\ $$$${S}_{\mathrm{1}} =\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{i}}{\mathrm{2}^{{i}} }=\mathrm{0}+\frac{\mathrm{1}}{\mathrm{2}\:}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{4}} }+… \\ $$$$\frac{{S}_{\mathrm{1}} }{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{4}} }+… \\ $$$${S}_{\mathrm{1}} −\frac{{S}_{\mathrm{1}} }{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+..=\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{1}\Rightarrow{S}_{\mathrm{1}} =\mathrm{2} \\ $$$${S}_{\mathrm{2}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+…=\mathrm{2} \\ $$$$\mathrm{2}{S}_{\mathrm{1}} +{S}_{\mathrm{2}} =\mathrm{6} \\ $$

Pin