Question Number 10133 by konen last updated on 26/Jan/17
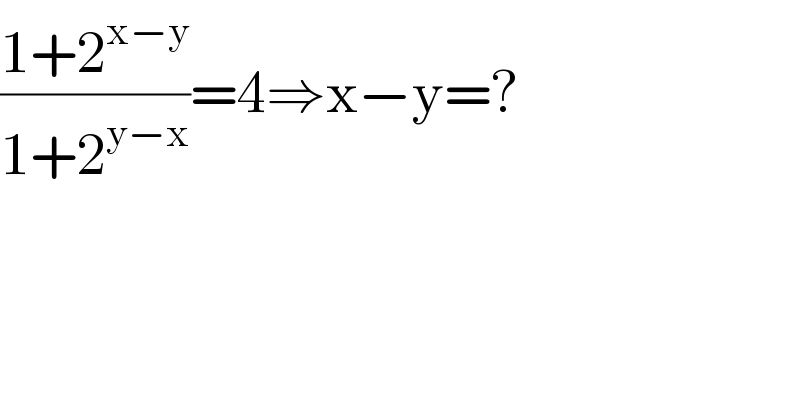
$$\frac{\mathrm{1}+\mathrm{2}^{\mathrm{x}−\mathrm{y}} }{\mathrm{1}+\mathrm{2}^{\mathrm{y}−\mathrm{x}} }=\mathrm{4}\Rightarrow\mathrm{x}−\mathrm{y}=? \\ $$
Answered by ridwan balatif last updated on 26/Jan/17
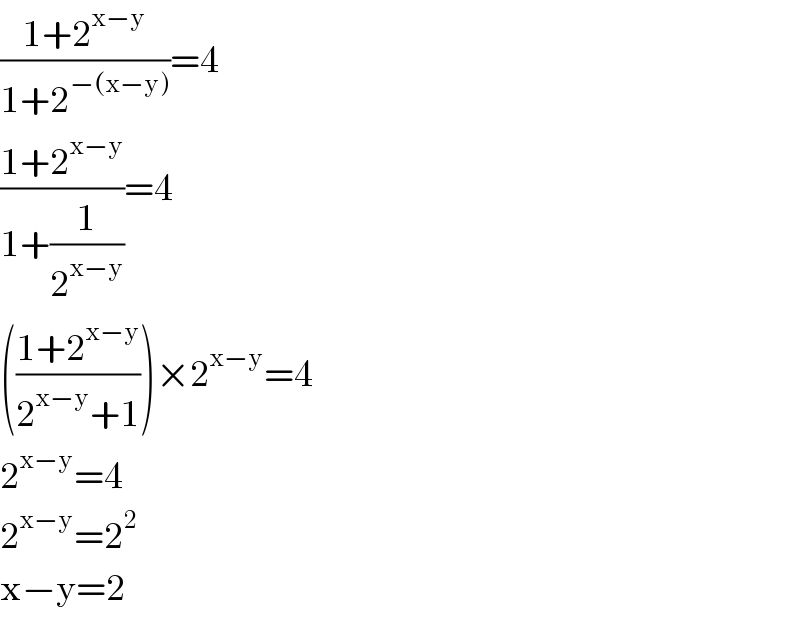
$$\frac{\mathrm{1}+\mathrm{2}^{\mathrm{x}−\mathrm{y}} }{\mathrm{1}+\mathrm{2}^{−\left(\mathrm{x}−\mathrm{y}\right)} }=\mathrm{4} \\ $$$$\frac{\mathrm{1}+\mathrm{2}^{\mathrm{x}−\mathrm{y}} }{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{x}−\mathrm{y}} }}=\mathrm{4} \\ $$$$\left(\frac{\mathrm{1}+\mathrm{2}^{\mathrm{x}−\mathrm{y}} }{\mathrm{2}^{\mathrm{x}−\mathrm{y}} +\mathrm{1}}\right)×\mathrm{2}^{\mathrm{x}−\mathrm{y}} =\mathrm{4} \\ $$$$\mathrm{2}^{\mathrm{x}−\mathrm{y}} =\mathrm{4} \\ $$$$\mathrm{2}^{\mathrm{x}−\mathrm{y}} =\mathrm{2}^{\mathrm{2}} \\ $$$$\mathrm{x}−\mathrm{y}=\mathrm{2} \\ $$
