Question Number 141599 by I want to learn more last updated on 20/May/21
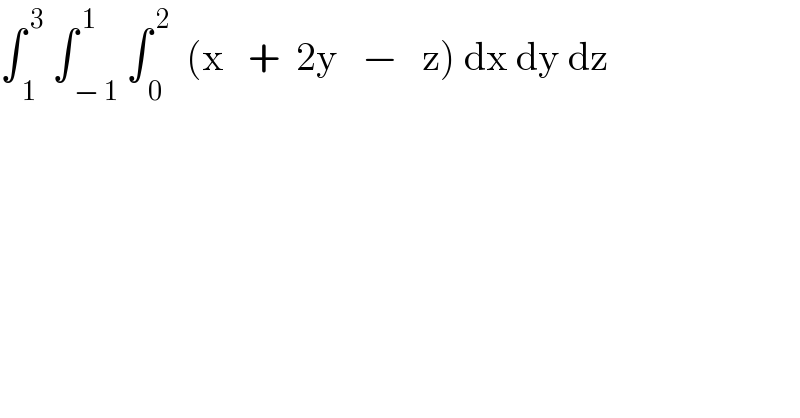
$$\int_{\:\mathrm{1}} ^{\:\mathrm{3}} \:\int_{\:−\:\mathrm{1}} ^{\:\mathrm{1}} \int_{\:\mathrm{0}} ^{\:\mathrm{2}} \:\:\left(\mathrm{x}\:\:\:+\:\:\mathrm{2y}\:\:\:−\:\:\:\mathrm{z}\right)\:\mathrm{dx}\:\mathrm{dy}\:\mathrm{dz} \\ $$
Commented by I want to learn more last updated on 21/May/21

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Answered by floor(10²Eta[1]) last updated on 21/May/21
![∫_1 ^3 ∫_(−1) ^1 [(x^2 /2)+2yx−zx]_0 ^2 dydz ∫_1 ^3 ∫_(−1) ^1 (2+4y−2z)dyxz ∫_1 ^3 [2y+2y^2 −2zy]_(−1) ^1 dz ∫_1 ^3 (4−4z)dz [4z−2z^2 ]_1 ^3 =−8](https://www.tinkutara.com/question/Q141601.png)
$$\int_{\mathrm{1}} ^{\mathrm{3}} \int_{−\mathrm{1}} ^{\mathrm{1}} \left[\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2yx}−\mathrm{zx}\right]_{\mathrm{0}} ^{\mathrm{2}} \mathrm{dydz} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{3}} \int_{−\mathrm{1}} ^{\mathrm{1}} \left(\mathrm{2}+\mathrm{4y}−\mathrm{2z}\right)\mathrm{dyxz} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{3}} \left[\mathrm{2y}+\mathrm{2y}^{\mathrm{2}} −\mathrm{2zy}\right]_{−\mathrm{1}} ^{\mathrm{1}} \mathrm{dz} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{3}} \left(\mathrm{4}−\mathrm{4z}\right)\mathrm{dz} \\ $$$$\left[\mathrm{4z}−\mathrm{2z}^{\mathrm{2}} \right]_{\mathrm{1}} ^{\mathrm{3}} =−\mathrm{8} \\ $$
