Menu Close

1-3-6-21-11-147-16-1029-21-7203-26-50421-

Tinku Tara 0 Comments
Pin




Question Number 139800 by bramlexs22 last updated on 01/May/21
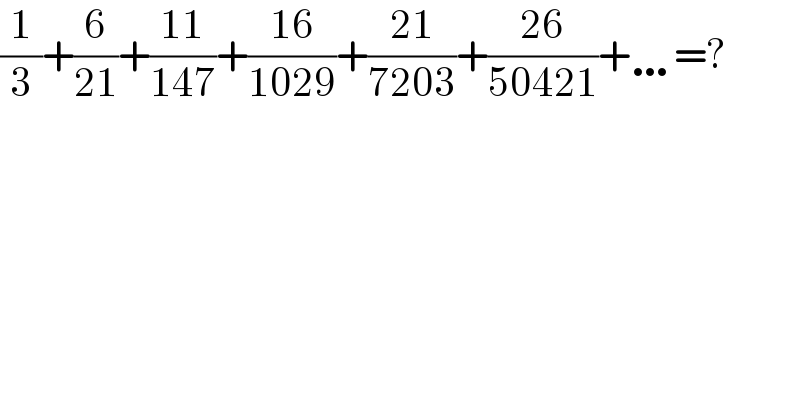
(1/3)+(6/(21))+((11)/(147))+((16)/(1029))+((21)/(7203))+((26)/(50421))+…=?
$$\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{6}}{\mathrm{21}}+\frac{\mathrm{11}}{\mathrm{147}}+\frac{\mathrm{16}}{\mathrm{1029}}+\frac{\mathrm{21}}{\mathrm{7203}}+\frac{\mathrm{26}}{\mathrm{50421}}+\ldots=? \\ $$
Answered by EDWIN88 last updated on 01/May/21
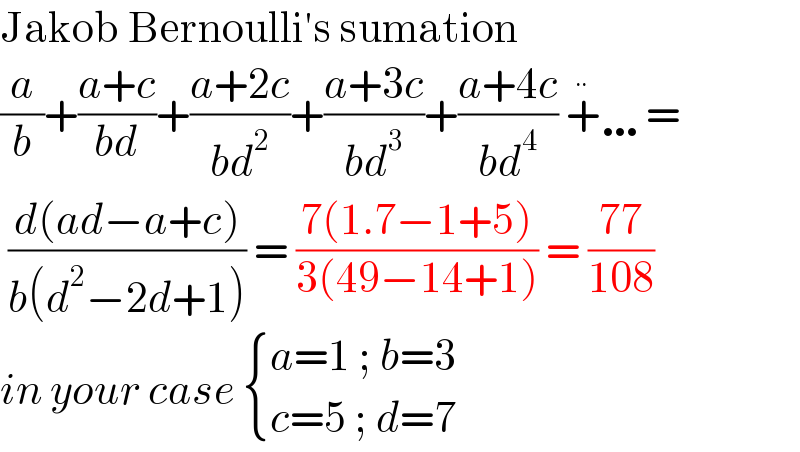
Jakob Bernoulli′s sumation (a/b)+((a+c)/(bd))+((a+2c)/(bd^2 ))+((a+3c)/(bd^3 ))+((a+4c)/(bd^4 )) +^ …= ((d(ad−a+c))/(b(d^2 −2d+1))) = ((7(1.7−1+5))/(3(49−14+1))) = ((77)/(108)) in your case { ((a=1 ; b=3)),((c=5 ; d=7)) :}
$$\mathrm{Jakob}\:\mathrm{Bernoulli}'\mathrm{s}\:\mathrm{sumation} \\ $$$$\frac{{a}}{{b}}+\frac{{a}+{c}}{{bd}}+\frac{{a}+\mathrm{2}{c}}{{bd}^{\mathrm{2}} }+\frac{{a}+\mathrm{3}{c}}{{bd}^{\mathrm{3}} }+\frac{{a}+\mathrm{4}{c}}{{bd}^{\mathrm{4}} }\:\ddot {+}\ldots= \\ $$$$\:\frac{{d}\left({ad}−{a}+{c}\right)}{{b}\left({d}^{\mathrm{2}} −\mathrm{2}{d}+\mathrm{1}\right)}\:=\:\frac{\mathrm{7}\left(\mathrm{1}.\mathrm{7}−\mathrm{1}+\mathrm{5}\right)}{\mathrm{3}\left(\mathrm{49}−\mathrm{14}+\mathrm{1}\right)}\:=\:\frac{\mathrm{77}}{\mathrm{108}} \\ $$$${in}\:{your}\:{case}\:\begin{cases}{{a}=\mathrm{1}\:;\:{b}=\mathrm{3}}\\{{c}=\mathrm{5}\:;\:{d}=\mathrm{7}}\end{cases} \\ $$
Commented by mohammad17 last updated on 01/May/21
sir whats low lf Jakob Bernoullis i want this low can you help me
$${sir}\:{whats}\:{low}\:{lf}\:{Jakob}\:{Bernoullis}\: \\ $$$${i}\:{want}\:{this}\:{low}\:{can}\:{you}\:{help}\:{me} \\ $$$$ \\ $$
Answered by qaz last updated on 01/May/21
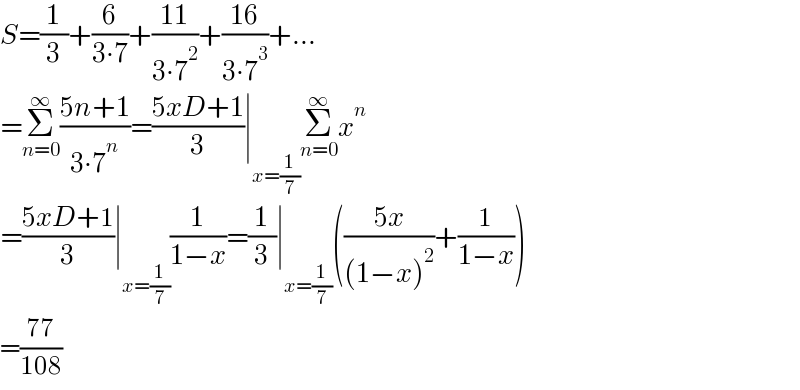
S=(1/3)+(6/(3∙7))+((11)/(3∙7^2 ))+((16)/(3∙7^3 ))+... =Σ_(n=0) ^∞ ((5n+1)/(3∙7^n ))=((5xD+1)/3)∣_(x=(1/7)) Σ_(n=0) ^∞ x^n =((5xD+1)/3)∣_(x=(1/7)) (1/(1−x))=(1/3)∣_(x=(1/7)) (((5x)/((1−x)^2 ))+(1/(1−x))) =((77)/(108))
$${S}=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{6}}{\mathrm{3}\centerdot\mathrm{7}}+\frac{\mathrm{11}}{\mathrm{3}\centerdot\mathrm{7}^{\mathrm{2}} }+\frac{\mathrm{16}}{\mathrm{3}\centerdot\mathrm{7}^{\mathrm{3}} }+… \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{5}{n}+\mathrm{1}}{\mathrm{3}\centerdot\mathrm{7}^{{n}} }=\frac{\mathrm{5}{xD}+\mathrm{1}}{\mathrm{3}}\mid_{{x}=\frac{\mathrm{1}}{\mathrm{7}}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} \\ $$$$=\frac{\mathrm{5}{xD}+\mathrm{1}}{\mathrm{3}}\mid_{{x}=\frac{\mathrm{1}}{\mathrm{7}}} \frac{\mathrm{1}}{\mathrm{1}−{x}}=\frac{\mathrm{1}}{\mathrm{3}}\mid_{{x}=\frac{\mathrm{1}}{\mathrm{7}}} \left(\frac{\mathrm{5}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}−{x}}\right) \\ $$$$=\frac{\mathrm{77}}{\mathrm{108}} \\ $$
Commented by bramlexs22 last updated on 01/May/21
answer ((77)/(108))
$$\mathrm{answer}\:\frac{\mathrm{77}}{\mathrm{108}} \\ $$
Commented by qaz last updated on 01/May/21
i got a mistake
$${i}\:{got}\:{a}\:{mistake} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *