Question Number 6351 by sanusihammed last updated on 24/Jun/16
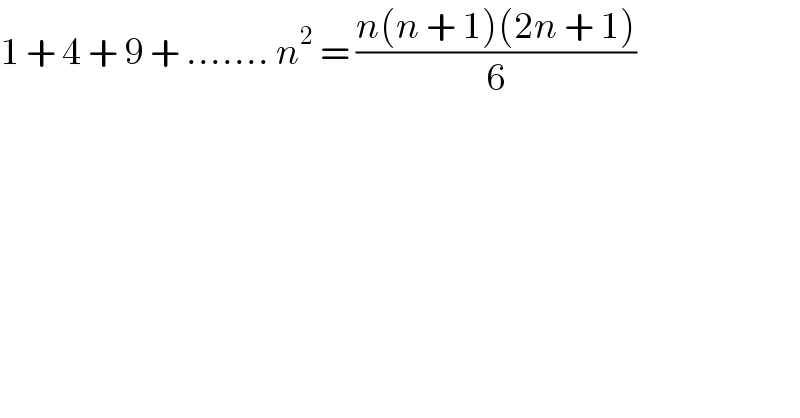
$$\mathrm{1}\:+\:\mathrm{4}\:+\:\mathrm{9}\:+\:…….\:{n}^{\mathrm{2}} \:=\:\frac{{n}\left({n}\:+\:\mathrm{1}\right)\left(\mathrm{2}{n}\:+\:\mathrm{1}\right)}{\mathrm{6}} \\ $$
Commented by prakash jain last updated on 24/Jun/16
![proving for k+1 assuming result for k ((k(k+1)(2k+1))/k)+(k+1)^2 =(((k+1))/6)(k(2k+1)+6k+6) =(((k+1))/6)(2k^2 +7k+6) =(((k+1))/6)(2k+3)(k+2)=(((k+1)(k+2)[2(k+1)+1])/6)](https://www.tinkutara.com/question/Q6361.png)
$${proving}\:{for}\:{k}+\mathrm{1}\:{assuming}\:{result}\:{for}\:{k} \\ $$$$\frac{{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}{{k}}+\left({k}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\frac{\left({k}+\mathrm{1}\right)}{\mathrm{6}}\left({k}\left(\mathrm{2}{k}+\mathrm{1}\right)+\mathrm{6}{k}+\mathrm{6}\right) \\ $$$$=\frac{\left({k}+\mathrm{1}\right)}{\mathrm{6}}\left(\mathrm{2}{k}^{\mathrm{2}} +\mathrm{7}{k}+\mathrm{6}\right) \\ $$$$=\frac{\left({k}+\mathrm{1}\right)}{\mathrm{6}}\left(\mathrm{2}{k}+\mathrm{3}\right)\left({k}+\mathrm{2}\right)=\frac{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)\left[\mathrm{2}\left({k}+\mathrm{1}\right)+\mathrm{1}\right]}{\mathrm{6}} \\ $$
