1-4-z-1-z-dz-

Question Number 138916 by mathsuji last updated on 20/Apr/21

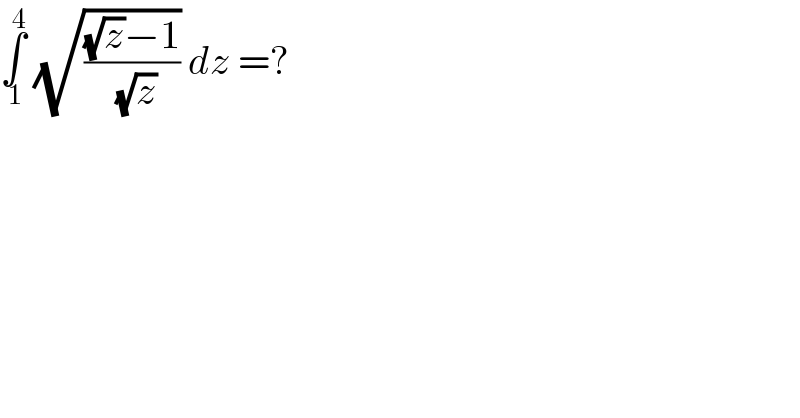
$$\underset{\:\mathrm{1}} {\overset{\:\mathrm{4}} {\int}}\:\sqrt{\frac{\sqrt{{z}}−\mathrm{1}}{\:\sqrt{{z}}}}\:{dz}\:=? \\ $$

Answered by bramlexs22 last updated on 20/Apr/21

(√(((√z)−1)/( (√z)))) = r ; (((√z) −1)/( (√z))) = r^2 → { ((z=1→r=0)),((z=4→r=(√(1/2)))) :} ⇒r^2 (√z) = (√z) −1 ⇒(√z) = (1/(1−r^2 )) ; z = (1−r^2 )^(−2) dz = −2(−2r)(1−r^2 )^(−3) dr dz = ((4r)/((1−r^2 )^3 )) dr I= ∫_0 ^((√2)/2) r(((4r)/((1−r^2 )^3 )))dr I=∫ 2r(((2r)/((1−r^2 )^3 )))dr by parts { ((u=2r⇒du=2dr)),((v=−∫ ((d(1−r^2 ))/((1−r^2 )^3 ))=(1/(2(1−r^2 )^2 )))) :} I= [ (r/((1−r^2 )^2 )) ]_0 ^((√2)/2) +∫_( 0) ^( ((√2)/2)) (dr/((1−r^2 )^2 )) now you can solve it

$$\sqrt{\frac{\sqrt{\mathrm{z}}−\mathrm{1}}{\:\sqrt{\mathrm{z}}}}\:=\:\mathrm{r}\:;\:\frac{\sqrt{\mathrm{z}}\:−\mathrm{1}}{\:\sqrt{\mathrm{z}}}\:=\:\mathrm{r}^{\mathrm{2}} \rightarrow\begin{cases}{\mathrm{z}=\mathrm{1}\rightarrow\mathrm{r}=\mathrm{0}}\\{\mathrm{z}=\mathrm{4}\rightarrow\mathrm{r}=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}\end{cases} \\ $$$$\Rightarrow\mathrm{r}^{\mathrm{2}} \:\sqrt{\mathrm{z}}\:=\:\sqrt{\mathrm{z}}\:−\mathrm{1} \\ $$$$\Rightarrow\sqrt{\mathrm{z}}\:=\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{r}^{\mathrm{2}} }\:;\:\mathrm{z}\:=\:\left(\mathrm{1}−\mathrm{r}^{\mathrm{2}} \right)^{−\mathrm{2}} \\ $$$$\mathrm{dz}\:=\:−\mathrm{2}\left(−\mathrm{2r}\right)\left(\mathrm{1}−\mathrm{r}^{\mathrm{2}} \right)^{−\mathrm{3}} \:\mathrm{dr} \\ $$$$\mathrm{dz}\:=\:\frac{\mathrm{4r}}{\left(\mathrm{1}−\mathrm{r}^{\mathrm{2}} \right)^{\mathrm{3}} }\:\mathrm{dr} \\ $$$$\mathrm{I}=\:\underset{\mathrm{0}} {\overset{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} {\int}}\:\mathrm{r}\left(\frac{\mathrm{4r}}{\left(\mathrm{1}−\mathrm{r}^{\mathrm{2}} \right)^{\mathrm{3}} }\right)\mathrm{dr} \\ $$$$\mathrm{I}=\int\:\mathrm{2r}\left(\frac{\mathrm{2r}}{\left(\mathrm{1}−\mathrm{r}^{\mathrm{2}} \right)^{\mathrm{3}} }\right)\mathrm{dr} \\ $$$$\mathrm{by}\:\mathrm{parts}\:\begin{cases}{\mathrm{u}=\mathrm{2r}\Rightarrow\mathrm{du}=\mathrm{2dr}}\\{\mathrm{v}=−\int\:\frac{\mathrm{d}\left(\mathrm{1}−\mathrm{r}^{\mathrm{2}} \right)}{\left(\mathrm{1}−\mathrm{r}^{\mathrm{2}} \right)^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\mathrm{r}^{\mathrm{2}} \right)^{\mathrm{2}} }}\end{cases} \\ $$$$\mathrm{I}=\:\left[\:\frac{\mathrm{r}}{\left(\mathrm{1}−\mathrm{r}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\right]_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} +\int_{\:\mathrm{0}} ^{\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \:\frac{\mathrm{dr}}{\left(\mathrm{1}−\mathrm{r}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{now}\:\mathrm{you}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{it} \\ $$

Answered by Ankushkumarparcha last updated on 20/Apr/21

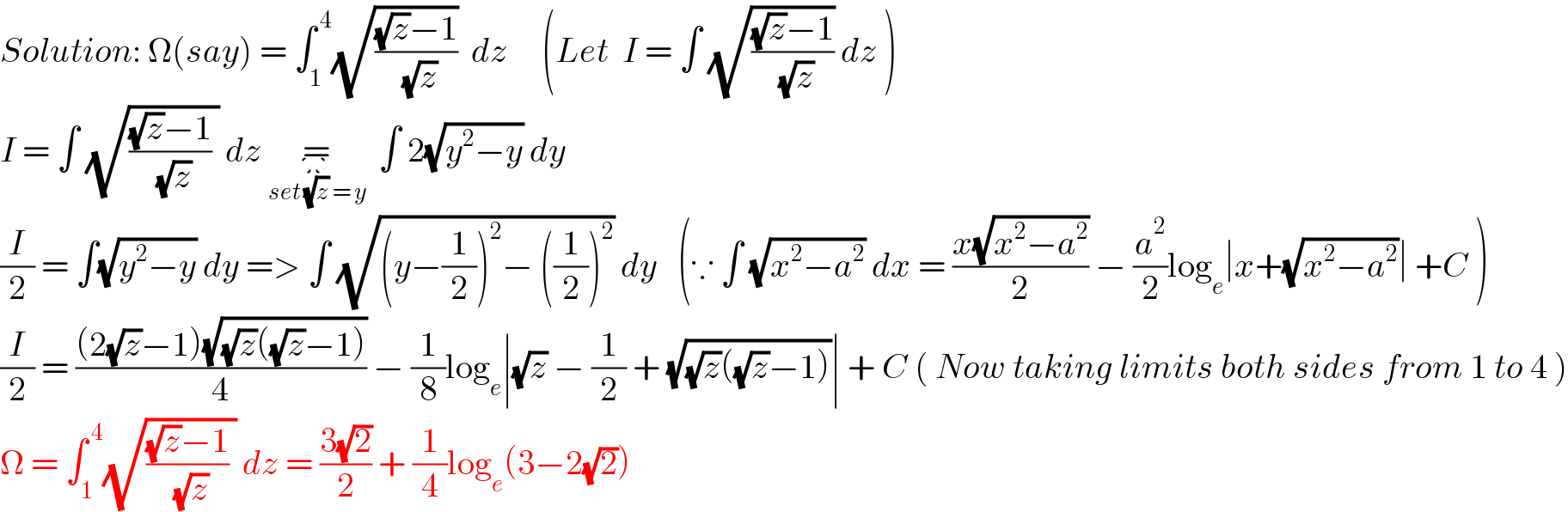
Solution: Ω(say) = ∫_1 ^( 4) (√(((√z)−1)/( (√z)))) dz (Let I = ∫ (√(((√z)−1)/( (√z)))) dz ) I = ∫ (√((((√z)−1)/( (√z))) )) dz =_(set (√z) = y) ∫ 2(√(y^2 −y)) dy (I/2) = ∫(√(y^2 −y)) dy => ∫ (√((y−(1/2))^2 − ((1/2))^2 )) dy (∵ ∫ (√(x^2 −a^2 )) dx = ((x(√(x^2 −a^2 )))/2) − (a^2 /2)log_e ∣x+(√(x^2 −a^2 ))∣ +C ) (I/2) = (((2(√z)−1)(√((√z)((√z)−1))))/4) − (1/8)log_e ∣(√z) − (1/2) + (√((√z)((√z)−1)))∣ + C ( Now taking limits both sides from 1 to 4 ) Ω = ∫_1 ^( 4) (√((((√z)−1)/( (√z))) )) dz = ((3(√2))/2) + (1/4)log_e (3−2(√2))

$${Solution}:\:\Omega\left({say}\right)\:=\:\int_{\mathrm{1}} ^{\:\mathrm{4}} \sqrt{\frac{\sqrt{{z}}−\mathrm{1}}{\:\sqrt{{z}}}}\:\:{dz}\:\:\:\:\:\left({Let}\:\:{I}\:=\:\int\:\sqrt{\frac{\sqrt{{z}}−\mathrm{1}}{\:\sqrt{{z}}}}\:{dz}\:\right) \\ $$$${I}\:=\:\int\:\sqrt{\frac{\sqrt{{z}}−\mathrm{1}}{\:\sqrt{{z}}}\:}\:{dz}\:\underset{{set}\:\sqrt{{z}}\:=\:{y}} {\underbrace{=}}\:\:\:\:\:\:\:\int\:\mathrm{2}\sqrt{{y}^{\mathrm{2}} −{y}}\:{dy} \\ $$$$\frac{{I}}{\mathrm{2}}\:=\:\int\sqrt{{y}^{\mathrm{2}} −{y}}\:{dy}\:=>\:\int\:\sqrt{\left({y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:{dy}\:\:\:\left(\because\:\int\:\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:{dx}\:=\:\frac{{x}\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{\mathrm{2}}\:−\:\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{log}_{{e}} \mid{x}+\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }\mid\:+{C}\:\right) \\ $$$$\frac{{I}}{\mathrm{2}}\:=\:\frac{\left(\mathrm{2}\sqrt{{z}}−\mathrm{1}\right)\sqrt{\sqrt{{z}}\left(\sqrt{{z}}−\mathrm{1}\right)}}{\mathrm{4}}\:−\:\frac{\mathrm{1}}{\mathrm{8}}\mathrm{log}_{{e}} \mid\sqrt{{z}}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\sqrt{\sqrt{{z}}\left(\sqrt{{z}}−\mathrm{1}\right)}\mid\:+\:{C}\:\left(\:{Now}\:{taking}\:{limits}\:{both}\:{sides}\:{from}\:\mathrm{1}\:{to}\:\mathrm{4}\:\right) \\ $$$$\Omega\:=\:\int_{\mathrm{1}} ^{\:\mathrm{4}} \sqrt{\frac{\sqrt{{z}}−\mathrm{1}}{\:\sqrt{{z}}}\:}\:{dz}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}_{{e}} \left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply