Question Number 136458 by aurpeyz last updated on 22/Mar/21
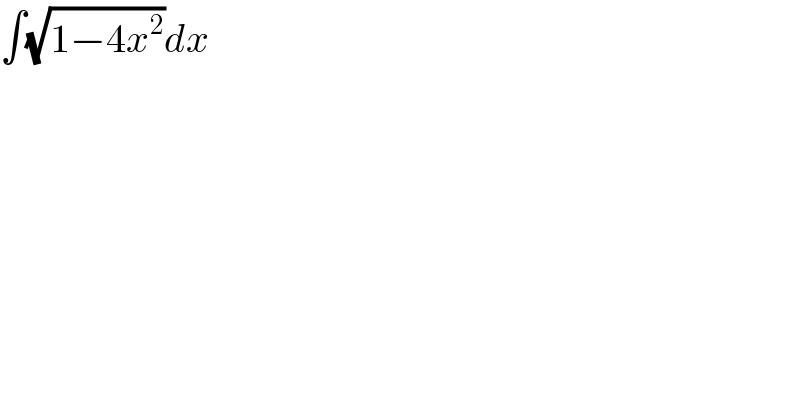
$$\int\sqrt{\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} }{dx} \\ $$
Answered by mathmax by abdo last updated on 22/Mar/21
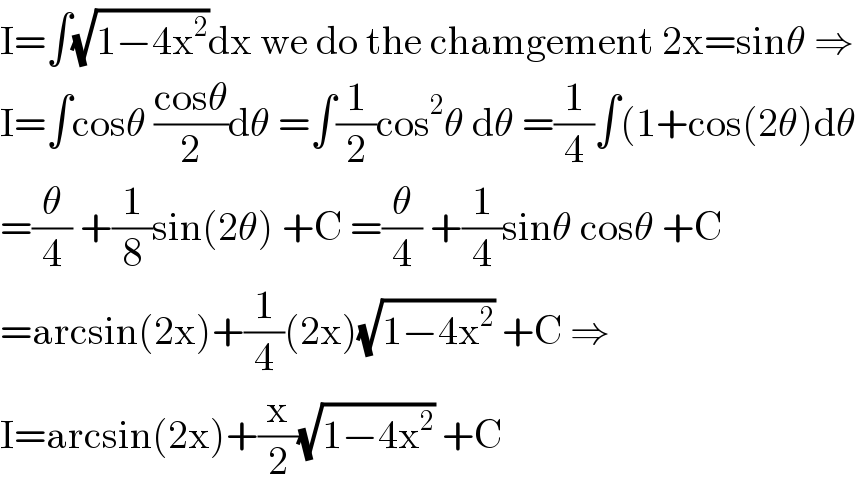
$$\mathrm{I}=\int\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{chamgement}\:\mathrm{2x}=\mathrm{sin}\theta\:\Rightarrow \\ $$$$\mathrm{I}=\int\mathrm{cos}\theta\:\frac{\mathrm{cos}\theta}{\mathrm{2}}\mathrm{d}\theta\:=\int\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \theta\:\mathrm{d}\theta\:=\frac{\mathrm{1}}{\mathrm{4}}\int\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)\mathrm{d}\theta\right. \\ $$$$=\frac{\theta}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\left(\mathrm{2}\theta\right)\:+\mathrm{C}\:=\frac{\theta}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\theta\:\mathrm{cos}\theta\:+\mathrm{C} \\ $$$$=\mathrm{arcsin}\left(\mathrm{2x}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2x}\right)\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\:+\mathrm{C}\:\Rightarrow \\ $$$$\mathrm{I}=\mathrm{arcsin}\left(\mathrm{2x}\right)+\frac{\mathrm{x}}{\mathrm{2}}\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\:+\mathrm{C} \\ $$
