Question Number 73358 by 07032041818 last updated on 10/Nov/19
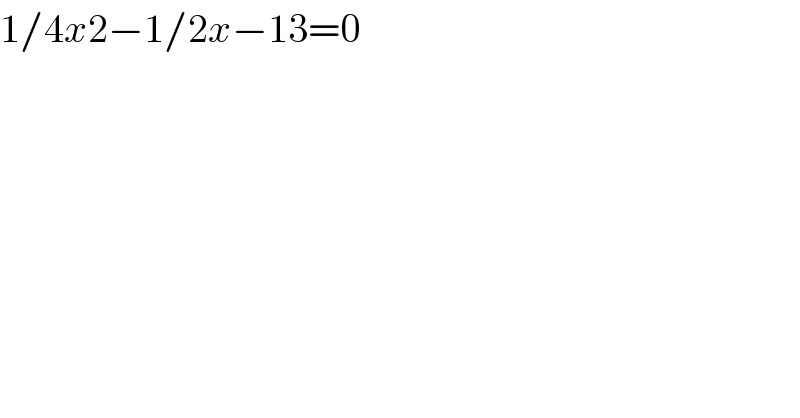
$$\mathrm{1}/\mathrm{4}{x}\mathrm{2}−\mathrm{1}/\mathrm{2}{x}−\mathrm{13}=\mathrm{0} \\ $$
Commented by MJS last updated on 10/Nov/19

$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{clear}\:\mathrm{whether}\:\mathrm{you}\:\mathrm{mean} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{x}−\mathrm{13}=\mathrm{0} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:×\mathrm{4} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{52}=\mathrm{0} \\ $$$${x}=\mathrm{1}\pm\sqrt{\mathrm{53}} \\ $$$$\mathrm{or}\:\mathrm{you}\:\mathrm{mean} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}{x}}−\mathrm{13}=\mathrm{0} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:×\left(−\mathrm{4}{x}^{\mathrm{2}} \right)/\mathrm{52} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{26}}{x}−\frac{\mathrm{1}}{\mathrm{52}}=\mathrm{0} \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{52}}\pm\frac{\sqrt{\mathrm{53}}}{\mathrm{52}} \\ $$
