1-5-1-5-

Question Number 2466 by prakash jain last updated on 20/Nov/15

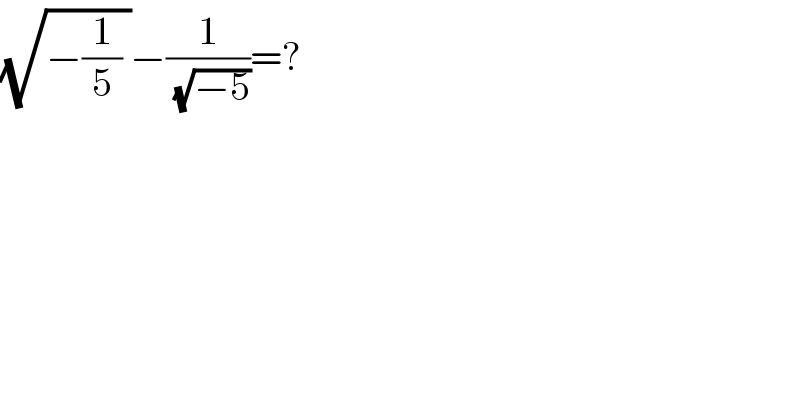
$$\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}\:}−\frac{\mathrm{1}}{\:\sqrt{−\mathrm{5}}}=? \\ $$

Answered by Yozzi last updated on 20/Nov/15

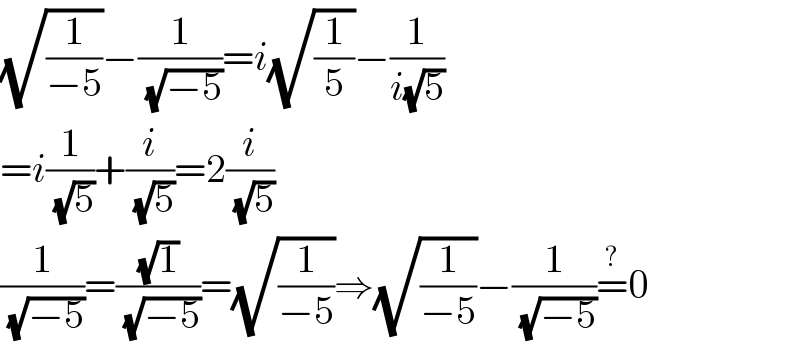
$$\sqrt{\frac{\mathrm{1}}{−\mathrm{5}}}−\frac{\mathrm{1}}{\:\sqrt{−\mathrm{5}}}={i}\sqrt{\frac{\mathrm{1}}{\mathrm{5}}}−\frac{\mathrm{1}}{{i}\sqrt{\mathrm{5}}} \\ $$$$={i}\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\frac{{i}}{\:\sqrt{\mathrm{5}}}=\mathrm{2}\frac{{i}}{\:\sqrt{\mathrm{5}}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{−\mathrm{5}}}=\frac{\sqrt{\mathrm{1}}}{\:\sqrt{−\mathrm{5}}}=\sqrt{\frac{\mathrm{1}}{−\mathrm{5}}}\Rightarrow\sqrt{\frac{\mathrm{1}}{−\mathrm{5}}}−\frac{\mathrm{1}}{\:\sqrt{−\mathrm{5}}}\overset{?} {=}\mathrm{0} \\ $$

Commented by prakash jain last updated on 20/Nov/15

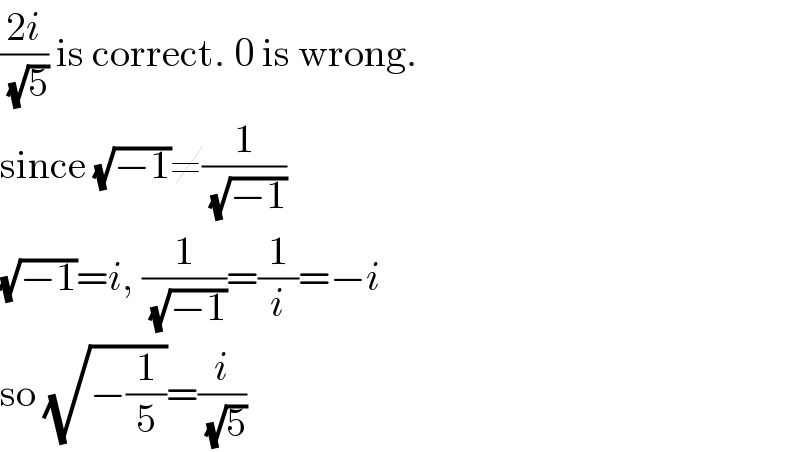
$$\frac{\mathrm{2}{i}}{\:\sqrt{\mathrm{5}}}\:\mathrm{is}\:\mathrm{correct}.\:\mathrm{0}\:\mathrm{is}\:\mathrm{wrong}. \\ $$$$\mathrm{since}\:\sqrt{−\mathrm{1}}\neq\frac{\mathrm{1}}{\:\sqrt{−\mathrm{1}}} \\ $$$$\sqrt{−\mathrm{1}}={i},\:\frac{\mathrm{1}}{\:\sqrt{−\mathrm{1}}}=\frac{\mathrm{1}}{{i}}=−{i} \\ $$$$\mathrm{so}\:\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}=\frac{{i}}{\:\sqrt{\mathrm{5}}} \\ $$

Commented by Yozzi last updated on 20/Nov/15

$${I}\:{see}.\: \\ $$

Answered by Rasheed Soomro last updated on 21/Nov/15

$$\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}\:}−\frac{\mathrm{1}}{\:\sqrt{−\mathrm{5}}}=? \\ $$$$\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}−\frac{\sqrt{\mathrm{1}}}{\:\sqrt{−\mathrm{5}}} \\ $$$$\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}−\sqrt{\frac{\mathrm{1}}{−\mathrm{5}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\because\:\frac{\sqrt{{a}}}{\:\sqrt{{b}}}=\sqrt{\frac{{a}}{{b}}} \\ $$$$\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}−\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\because\:\frac{+{ve}}{−{ve}}=−{ve} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\because{a}−{a}=\mathrm{0} \\ $$$${Where}\:{is}\:{logical}\:{mistake}? \\ $$

Commented by Filup last updated on 21/Nov/15

$$\mathrm{It}\:\mathrm{has}\:\mathrm{to}\:\mathrm{do}\:\mathrm{with}\:\mathrm{the}\:\mathrm{laws}\:\mathrm{of}\:\mathrm{complex}\:\mathrm{radicals}. \\ $$$$ \\ $$$$\mathrm{e}.\mathrm{g}. \\ $$$$\mathrm{1}\neq\sqrt{\left(−\mathrm{1}\right)\left(−\mathrm{1}\right)}=\sqrt{−\mathrm{1}}\sqrt{−\mathrm{1}}={i}^{\mathrm{2}} =−\mathrm{1} \\ $$$${Which}\:{is}\:{incorrect} \\ $$$$ \\ $$$$\sqrt{{a}}×\sqrt{{b}}\neq\sqrt{−{a}}×\sqrt{−{b}} \\ $$$$\sqrt{{a}}×\sqrt{−{b}}\neq\sqrt{−{a}}×\sqrt{{b}}\:\:\:\:\left(\mathrm{in}\:\mathrm{some}\:\mathrm{situations}\right) \\ $$$$ \\ $$$${such}\:{as}: \\ $$$$\mathrm{for}:\:\:\:\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}−\frac{\mathrm{1}}{\:\sqrt{−\mathrm{5}}}\Rightarrow\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}\neq\frac{\mathrm{1}}{\:\sqrt{−\mathrm{5}}} \\ $$

Commented by Rasheed Soomro last updated on 21/Nov/15

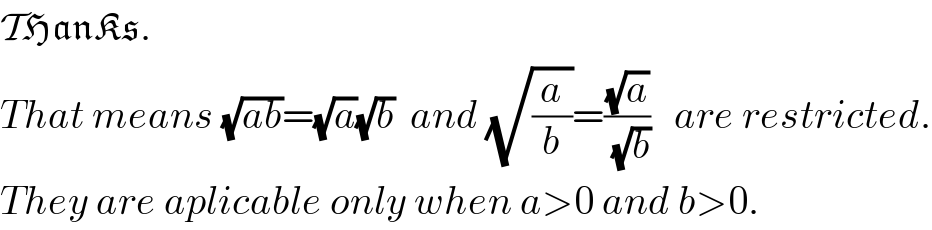
$$\mathcal{T}\mathfrak{HanKs}. \\ $$$${That}\:{means}\:\sqrt{{ab}}=\sqrt{{a}}\sqrt{{b}}\:\:{and}\:\sqrt{\frac{{a}}{{b}}}=\frac{\sqrt{{a}}}{\:\sqrt{{b}}}\:\:\:{are}\:{restricted}. \\ $$$${They}\:{are}\:{aplicable}\:{only}\:{when}\:{a}>\mathrm{0}\:{and}\:{b}>\mathrm{0}. \\ $$

Commented by Filup last updated on 21/Nov/15

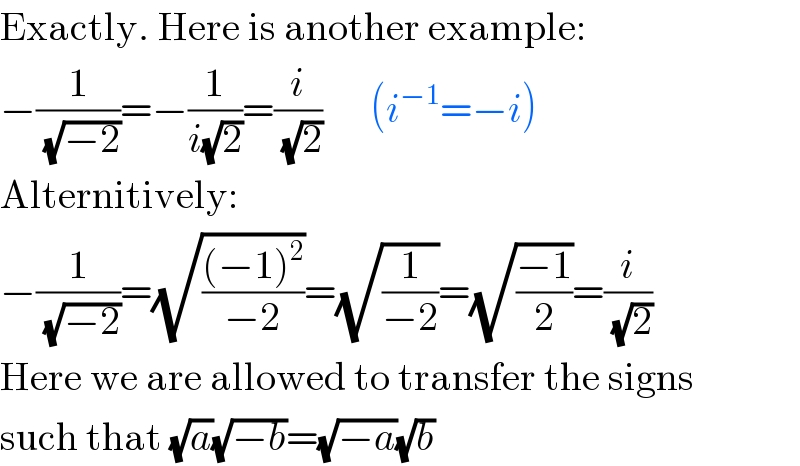
$$\mathrm{Exactly}.\:\mathrm{Here}\:\mathrm{is}\:\mathrm{another}\:\mathrm{example}: \\ $$$$−\frac{\mathrm{1}}{\:\sqrt{−\mathrm{2}}}=−\frac{\mathrm{1}}{{i}\sqrt{\mathrm{2}}}=\frac{{i}}{\:\sqrt{\mathrm{2}}}\:\:\:\:\:\:\left({i}^{−\mathrm{1}} =−{i}\right) \\ $$$$\mathrm{Alternitively}: \\ $$$$−\frac{\mathrm{1}}{\:\sqrt{−\mathrm{2}}}=\sqrt{\frac{\left(−\mathrm{1}\right)^{\mathrm{2}} }{−\mathrm{2}}}=\sqrt{\frac{\mathrm{1}}{−\mathrm{2}}}=\sqrt{\frac{−\mathrm{1}}{\mathrm{2}}}=\frac{{i}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{Here}\:\mathrm{we}\:\mathrm{are}\:\mathrm{allowed}\:\mathrm{to}\:\mathrm{transfer}\:\mathrm{the}\:\mathrm{signs} \\ $$$$\mathrm{such}\:\mathrm{that}\:\sqrt{{a}}\sqrt{−{b}}=\sqrt{−{a}}\sqrt{{b}} \\ $$

Commented by Filup last updated on 21/Nov/15

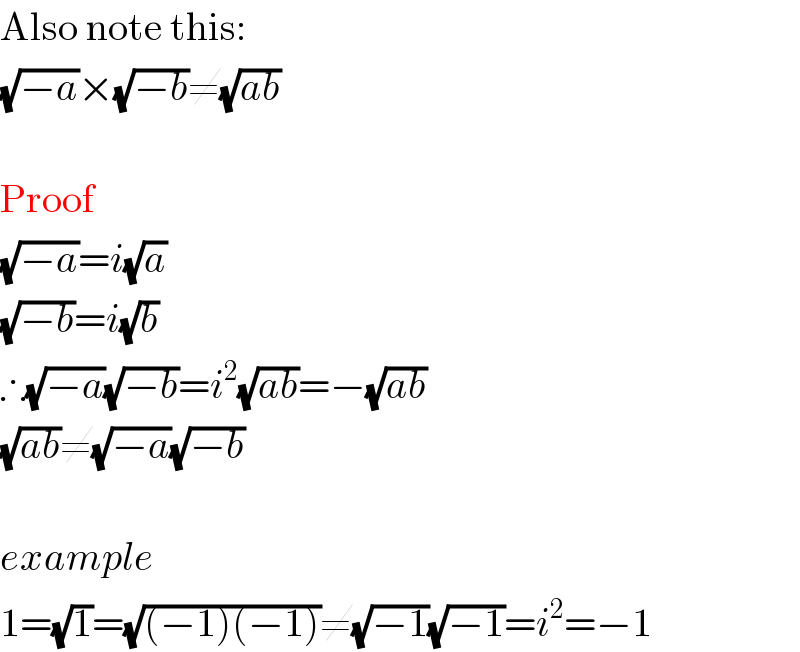
$$\mathrm{Also}\:\mathrm{note}\:\mathrm{this}: \\ $$$$\sqrt{−{a}}×\sqrt{−{b}}\neq\sqrt{{ab}} \\ $$$$ \\ $$$$\mathrm{Proof} \\ $$$$\sqrt{−{a}}={i}\sqrt{{a}} \\ $$$$\sqrt{−{b}}={i}\sqrt{{b}} \\ $$$$\therefore\sqrt{−{a}}\sqrt{−{b}}={i}^{\mathrm{2}} \sqrt{{ab}}=−\sqrt{{ab}} \\ $$$$\sqrt{{ab}}\neq\sqrt{−{a}}\sqrt{−{b}} \\ $$$$ \\ $$$${example} \\ $$$$\mathrm{1}=\sqrt{\mathrm{1}}=\sqrt{\left(−\mathrm{1}\right)\left(−\mathrm{1}\right)}\neq\sqrt{−\mathrm{1}}\sqrt{−\mathrm{1}}={i}^{\mathrm{2}} =−\mathrm{1} \\ $$

Commented by Rasheed Soomro last updated on 22/Nov/15

$${Is}\:\sqrt{−{a}}\sqrt{{b}}\:=\sqrt{−{ab}\:}?\:\:\:\:\:\:\:\:\:\left[\:{a},{b}>\mathrm{0}\right] \\ $$

Answered by Filup last updated on 21/Nov/15

$$\mathrm{Follwing}\:\mathrm{the}\:\mathrm{laws}\:\mathrm{of}\:\mathrm{complex}\:\mathrm{radicles}, \\ $$$$\mathrm{both}\:\mathrm{answers}\:\mathrm{of}\:\:\frac{\mathrm{2}{i}}{\:\sqrt{\mathrm{5}}}\:\:\mathrm{and}\:\mathrm{0}\:{are}\:{correct}. \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{belive}\:\mathrm{that}\:\mathrm{we}\:\mathrm{have}\:\mathrm{two}\:\mathrm{solutions}. \\ $$$$\frac{\mathrm{2}{i}}{\:\sqrt{\mathrm{5}}}\:\mathrm{is}\:\mathrm{our}\:\mathrm{complex}\:\mathrm{solution}\:\:\left(\Im\left({z}\right)=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right) \\ $$$$\mathrm{0}\:\mathrm{is}\:\mathrm{our}\:\mathrm{real}\:\mathrm{solution} \\ $$$$ \\ $$$$\mathrm{If}\:\:{z}=\Re\left({z}\right)+\Im\left({z}\right)\:\:\mathrm{we}\:\mathrm{have}: \\ $$$${z}=\mathrm{0}+\frac{\mathrm{2}{i}}{\:\sqrt{\mathrm{5}}} \\ $$

Commented by Rasheed Soomro last updated on 22/Nov/15

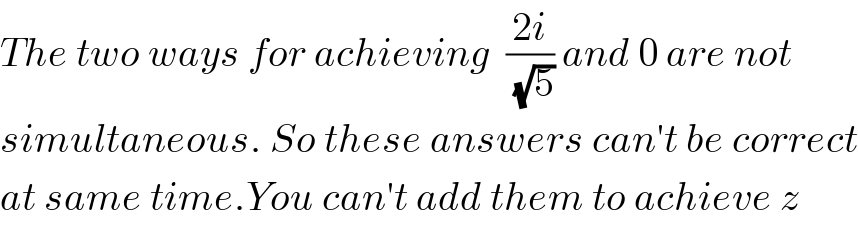
$${The}\:{two}\:{ways}\:{for}\:{achieving}\:\:\frac{\mathrm{2}{i}}{\:\sqrt{\mathrm{5}}}\:{and}\:\mathrm{0}\:{are}\:{not} \\ $$$${simultaneous}.\:{So}\:{these}\:{answers}\:{can}'{t}\:{be}\:{correct} \\ $$$${at}\:{same}\:{time}.{You}\:{can}'{t}\:{add}\:{them}\:{to}\:{achieve}\:{z} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com