Question Number 136968 by Eric002 last updated on 28/Mar/21
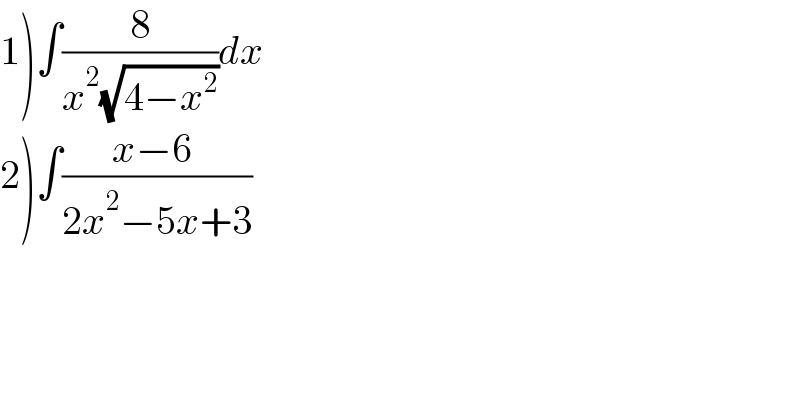
$$\left.\mathrm{1}\right)\int\frac{\mathrm{8}}{{x}^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{dx} \\ $$$$\left.\mathrm{2}\right)\int\frac{{x}−\mathrm{6}\:}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}} \\ $$
Answered by EDWIN88 last updated on 28/Mar/21
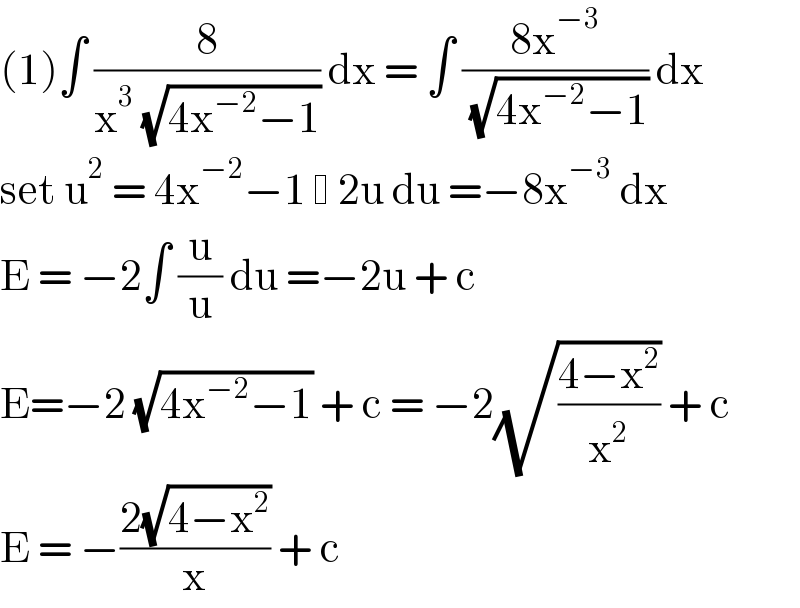
$$\left(\mathrm{1}\right)\int\:\frac{\mathrm{8}}{\mathrm{x}^{\mathrm{3}} \:\sqrt{\mathrm{4x}^{−\mathrm{2}} −\mathrm{1}}}\:\mathrm{dx}\:=\:\int\:\frac{\mathrm{8x}^{−\mathrm{3}} }{\:\sqrt{\mathrm{4x}^{−\mathrm{2}} −\mathrm{1}}}\:\mathrm{dx} \\ $$$$\mathrm{set}\:\mathrm{u}^{\mathrm{2}} \:=\:\mathrm{4x}^{−\mathrm{2}} −\mathrm{1}\: \:\mathrm{2u}\:\mathrm{du}\:=−\mathrm{8x}^{−\mathrm{3}} \:\mathrm{dx} \\ $$$$\mathrm{E}\:=\:−\mathrm{2}\int\:\frac{\mathrm{u}}{\mathrm{u}}\:\mathrm{du}\:=−\mathrm{2u}\:+\:\mathrm{c}\: \\ $$$$\mathrm{E}=−\mathrm{2}\:\sqrt{\mathrm{4x}^{−\mathrm{2}} −\mathrm{1}}\:+\:\mathrm{c}\:=\:−\mathrm{2}\sqrt{\frac{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }}\:+\:\mathrm{c} \\ $$$$\mathrm{E}\:=\:−\frac{\mathrm{2}\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}}\:+\:\mathrm{c}\: \\ $$
Answered by EDWIN88 last updated on 28/Mar/21
![(2)E=∫ ((x−6)/((2x+1)(x−3))) dx Partial fraction ((x−6)/(2x^2 −5x+3)) = (p/(2x+1)) + (q/(x−3)) where { ((p=[((x−6)/(x−3)) ] _(x=−(1/2)) = ((−13)/(−7))=((13)/7))),((q=[((x−6)/(2x+1)) ]_(x=3) =−(3/7))) :} E=((13)/7)∫ (dx/(2x+1)) −(3/7)∫ (dx/(x−3)) E=((13)/(14)) ln ∣2x+1∣−(3/7) ln ∣x−3∣ + c](https://www.tinkutara.com/question/Q136975.png)
$$\left(\mathrm{2}\right)\mathrm{E}=\int\:\frac{\mathrm{x}−\mathrm{6}}{\left(\mathrm{2x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{3}\right)}\:\mathrm{dx}\: \\ $$$$\mathrm{Partial}\:\mathrm{fraction}\: \frac{\mathrm{x}−\mathrm{6}}{\mathrm{2x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{3}}\:=\:\frac{\mathrm{p}}{\mathrm{2x}+\mathrm{1}}\:+\:\frac{\mathrm{q}}{\mathrm{x}−\mathrm{3}} \\ $$$$\mathrm{where}\:\begin{cases}{\mathrm{p}=\left[\frac{\mathrm{x}−\mathrm{6}}{\mathrm{x}−\mathrm{3}}\:\right]\:_{\mathrm{x}=−\frac{\mathrm{1}}{\mathrm{2}}} =\:\frac{−\mathrm{13}}{−\mathrm{7}}=\frac{\mathrm{13}}{\mathrm{7}}}\\{\mathrm{q}=\left[\frac{\mathrm{x}−\mathrm{6}}{\mathrm{2x}+\mathrm{1}}\:\right]_{\mathrm{x}=\mathrm{3}} =−\frac{\mathrm{3}}{\mathrm{7}}}\end{cases} \\ $$$$\mathrm{E}=\frac{\mathrm{13}}{\mathrm{7}}\int\:\frac{\mathrm{dx}}{\mathrm{2x}+\mathrm{1}}\:−\frac{\mathrm{3}}{\mathrm{7}}\int\:\frac{\mathrm{dx}}{\mathrm{x}−\mathrm{3}} \\ $$$$\mathrm{E}=\frac{\mathrm{13}}{\mathrm{14}}\:\mathrm{ln}\:\mid\mathrm{2x}+\mathrm{1}\mid−\frac{\mathrm{3}}{\mathrm{7}}\:\mathrm{ln}\:\mid\mathrm{x}−\mathrm{3}\mid\:+\:\mathrm{c}\: \\ $$
Answered by mathmax by abdo last updated on 28/Mar/21
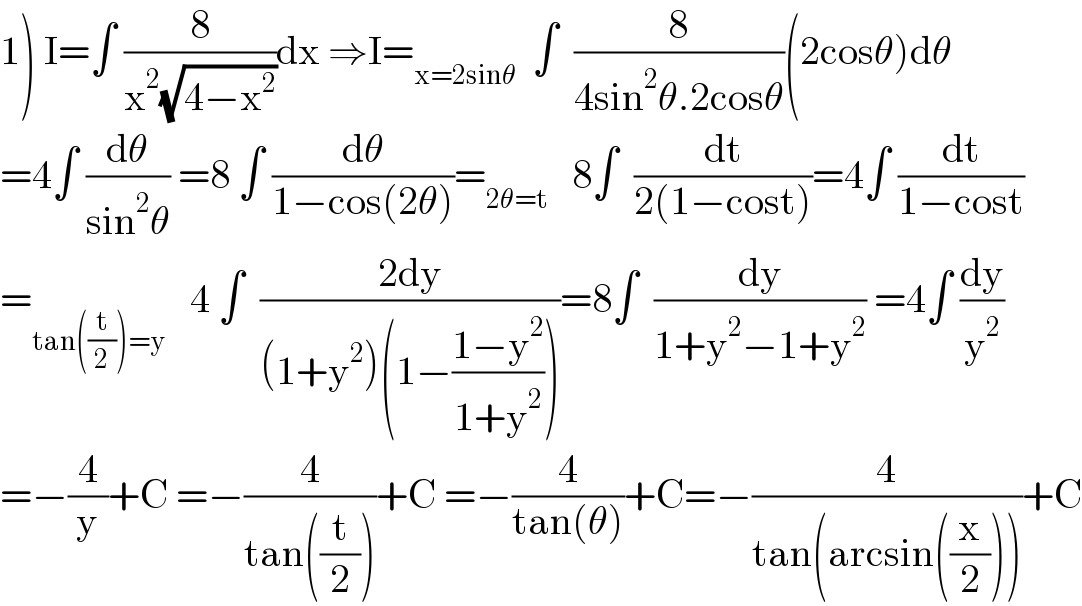
$$\left.\mathrm{1}\right)\:\mathrm{I}=\int\:\frac{\mathrm{8}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:\Rightarrow\mathrm{I}=_{\mathrm{x}=\mathrm{2sin}\theta} \:\:\int\:\:\frac{\mathrm{8}}{\mathrm{4sin}^{\mathrm{2}} \theta.\mathrm{2cos}\theta}\left(\mathrm{2cos}\theta\right)\mathrm{d}\theta \\ $$$$=\mathrm{4}\int\:\frac{\mathrm{d}\theta}{\mathrm{sin}^{\mathrm{2}} \theta}\:=\mathrm{8}\:\int\:\frac{\mathrm{d}\theta}{\mathrm{1}−\mathrm{cos}\left(\mathrm{2}\theta\right)}=_{\mathrm{2}\theta=\mathrm{t}} \:\:\:\mathrm{8}\int\:\:\frac{\mathrm{dt}}{\mathrm{2}\left(\mathrm{1}−\mathrm{cost}\right)}=\mathrm{4}\int\:\frac{\mathrm{dt}}{\mathrm{1}−\mathrm{cost}} \\ $$$$=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{y}} \:\:\:\mathrm{4}\:\int\:\:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }\right)}=\mathrm{8}\int\:\:\frac{\mathrm{dy}}{\mathrm{1}+\mathrm{y}^{\mathrm{2}} −\mathrm{1}+\mathrm{y}^{\mathrm{2}} }\:=\mathrm{4}\int\:\frac{\mathrm{dy}}{\mathrm{y}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{4}}{\mathrm{y}}+\mathrm{C}\:=−\frac{\mathrm{4}}{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)}+\mathrm{C}\:=−\frac{\mathrm{4}}{\mathrm{tan}\left(\theta\right)}+\mathrm{C}=−\frac{\mathrm{4}}{\mathrm{tan}\left(\mathrm{arcsin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)}+\mathrm{C} \\ $$
