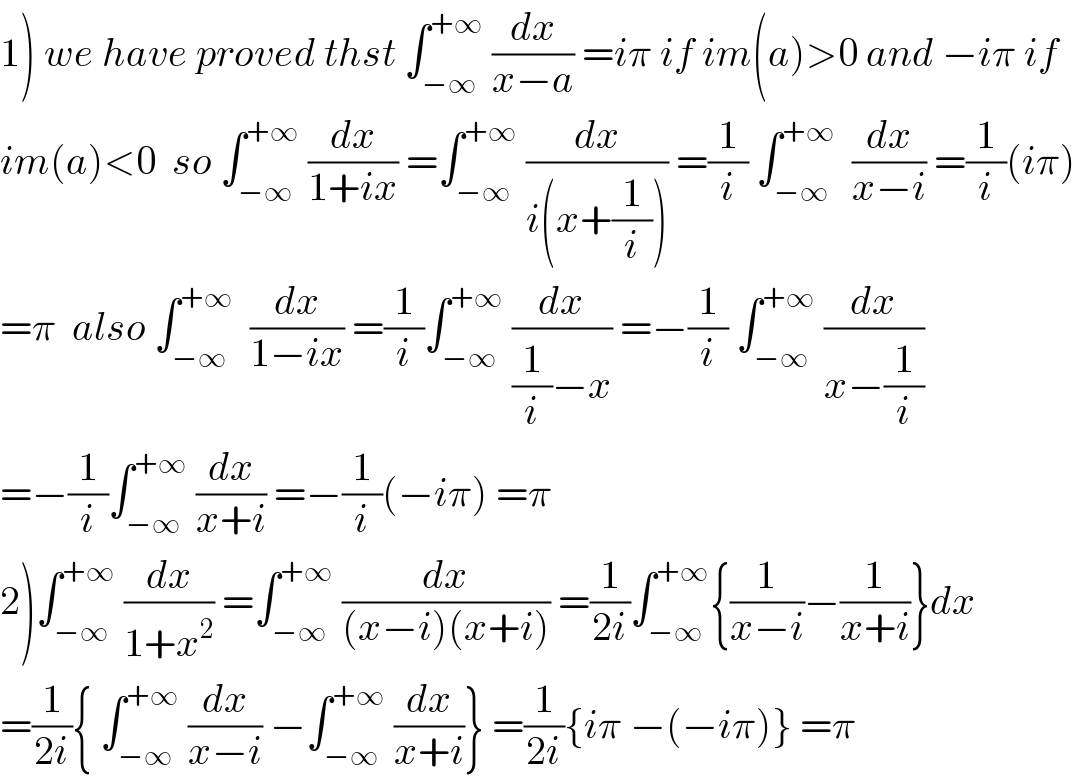Menu Close

1-calculate-dx-1-ix-and-dx-1-ix-2-deduce-the-value-of-dx-1-x-2-3-calculate-dx-1-ix-2-and-dx-1-ix-2-4-deduce-the-value

Tinku Tara
Pin




Question Number 65837 by mathmax by abdo last updated on 04/Aug/19
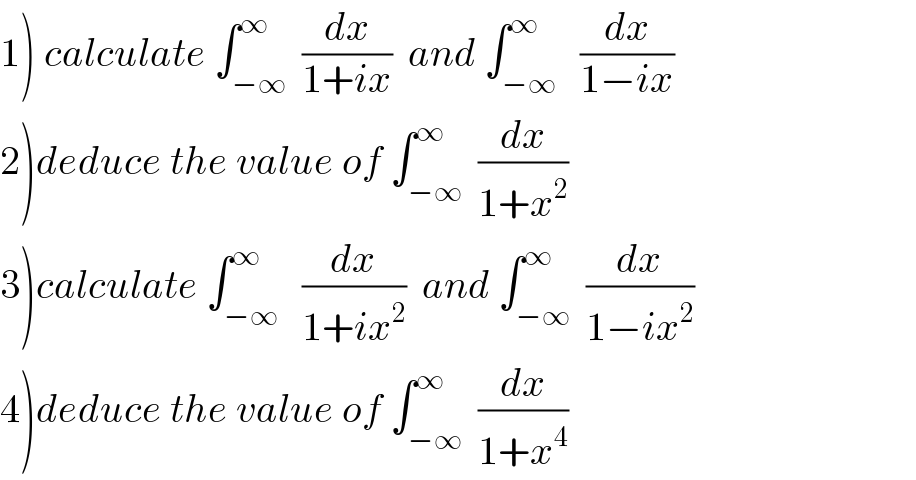
1) calculate ∫_(−∞) ^∞ (dx/(1+ix)) and ∫_(−∞) ^∞ (dx/(1−ix)) 2)deduce the value of ∫_(−∞) ^∞ (dx/(1+x^2 )) 3)calculate ∫_(−∞) ^∞ (dx/(1+ix^2 )) and ∫_(−∞) ^∞ (dx/(1−ix^2 )) 4)deduce the value of ∫_(−∞) ^∞ (dx/(1+x^4 ))
$$\left.\mathrm{1}\right)\:{calculate}\:\int_{−\infty} ^{\infty} \:\frac{{dx}}{\mathrm{1}+{ix}}\:\:{and}\:\int_{−\infty} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}−{ix}} \\ $$$$\left.\mathrm{2}\right){deduce}\:{the}\:{value}\:{of}\:\int_{−\infty} ^{\infty} \:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right){calculate}\:\int_{−\infty} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}+{ix}^{\mathrm{2}} }\:\:{and}\:\int_{−\infty} ^{\infty} \:\frac{{dx}}{\mathrm{1}−{ix}^{\mathrm{2}} } \\ $$$$\left.\mathrm{4}\right){deduce}\:{the}\:{value}\:{of}\:\int_{−\infty} ^{\infty} \:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} } \\ $$
Commented by ~ À ® @ 237 ~ last updated on 05/Aug/19
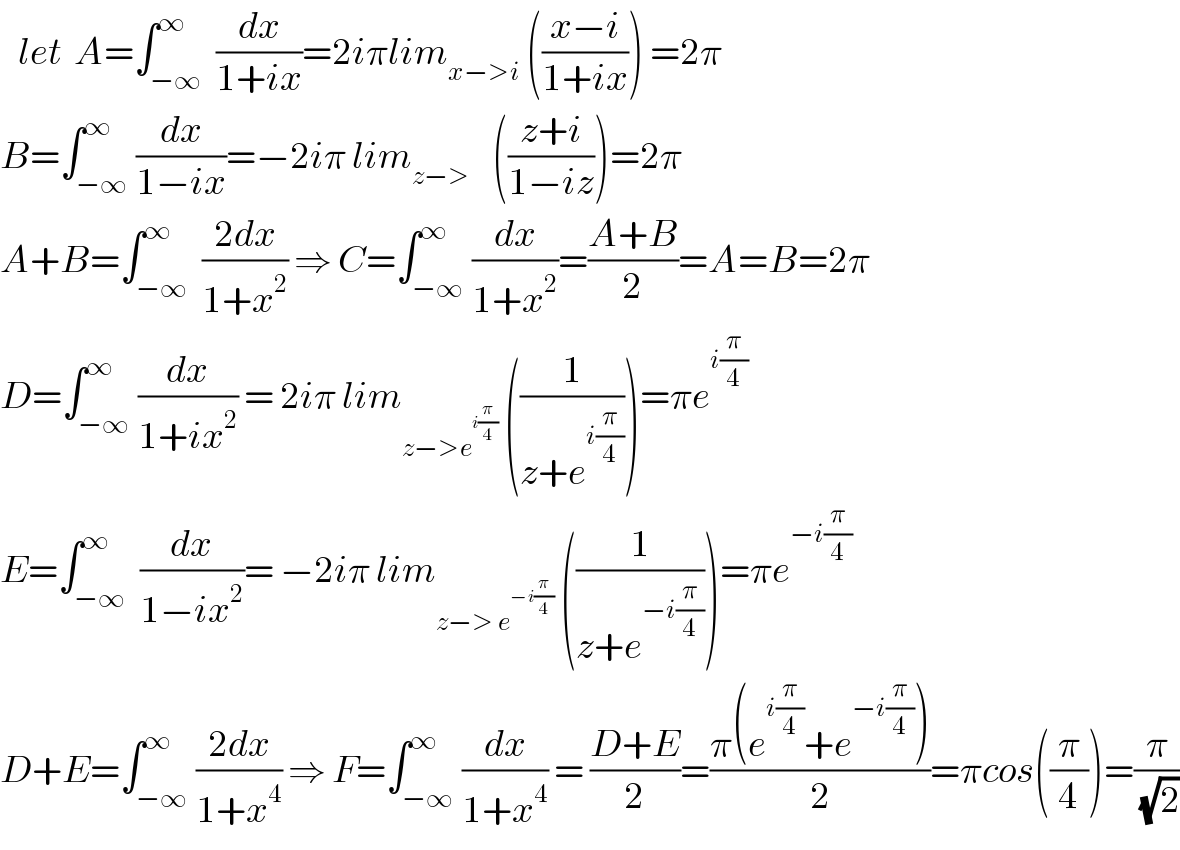
let A=∫_(−∞) ^∞ (dx/(1+ix))=2iπlim_(x−>i) (((x−i)/(1+ix))) =2π B=∫_(−∞) ^∞ (dx/(1−ix))=−2iπ lim_(z−> ) (((z+i)/(1−iz)))=2π A+B=∫_(−∞) ^∞ ((2dx)/(1+x^2 )) ⇒ C=∫_(−∞) ^∞ (dx/(1+x^2 ))=((A+B)/2)=A=B=2π D=∫_(−∞) ^∞ (dx/(1+ix^2 )) = 2iπ lim_(z−>e^(i(π/4)) ) ((1/(z+e^(i(π/4)) )))=πe^(i(π/4)) E=∫_(−∞) ^∞ (dx/(1−ix^2 ))= −2iπ lim_(z−> e^(−i(π/4)) ) ((1/(z+e^(−i(π/4)) )))=πe^(−i(π/4)) D+E=∫_(−∞) ^∞ ((2dx)/(1+x^4 )) ⇒ F=∫_(−∞) ^∞ (dx/(1+x^4 )) = ((D+E)/2)=((π(e^(i(π/4)) +e^(−i(π/4)) ))/2)=πcos((π/4))=(π/( (√2)))
$$\:\:\:{let}\:\:{A}=\int_{−\infty} ^{\infty} \:\frac{{dx}}{\mathrm{1}+{ix}}=\mathrm{2}{i}\pi{lim}_{{x}−>{i}} \:\left(\frac{{x}−{i}}{\mathrm{1}+{ix}}\right)\:=\mathrm{2}\pi \\ $$$${B}=\int_{−\infty} ^{\infty} \frac{{dx}}{\mathrm{1}−{ix}}=−\mathrm{2}{i}\pi\:{lim}_{{z}−>\:\:\:\:} \:\left(\frac{{z}+{i}}{\mathrm{1}−{iz}}\right)=\mathrm{2}\pi \\ $$$${A}+{B}=\int_{−\infty} ^{\infty} \:\frac{\mathrm{2}{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow\:{C}=\int_{−\infty} ^{\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }=\frac{{A}+{B}}{\mathrm{2}}={A}={B}=\mathrm{2}\pi \\ $$$${D}=\int_{−\infty} ^{\infty} \frac{{dx}}{\mathrm{1}+{ix}^{\mathrm{2}} }\:=\:\mathrm{2}{i}\pi\:{lim}_{{z}−>{e}^{{i}\frac{\pi}{\mathrm{4}}} } \:\left(\frac{\mathrm{1}}{{z}+{e}^{{i}\frac{\pi}{\mathrm{4}}} }\right)=\pi{e}^{{i}\frac{\pi}{\mathrm{4}}} \\ $$$${E}=\int_{−\infty} ^{\infty} \:\frac{{dx}}{\mathrm{1}−{ix}^{\mathrm{2}} }=\:−\mathrm{2}{i}\pi\:{lim}_{{z}−>\:{e}^{−{i}\frac{\pi}{\mathrm{4}}} } \:\left(\frac{\mathrm{1}}{{z}+{e}^{−{i}\frac{\pi}{\mathrm{4}}} }\right)=\pi{e}^{−{i}\frac{\pi}{\mathrm{4}}} \: \\ $$$${D}+{E}=\int_{−\infty} ^{\infty} \frac{\mathrm{2}{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }\:\Rightarrow\:{F}=\int_{−\infty} ^{\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }\:=\:\frac{{D}+{E}}{\mathrm{2}}=\frac{\pi\left({e}^{{i}\frac{\pi}{\mathrm{4}}} +{e}^{−{i}\frac{\pi}{\mathrm{4}}} \right)}{\mathrm{2}}=\pi{cos}\left(\frac{\pi}{\mathrm{4}}\right)=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by mathmax by abdo last updated on 05/Aug/19
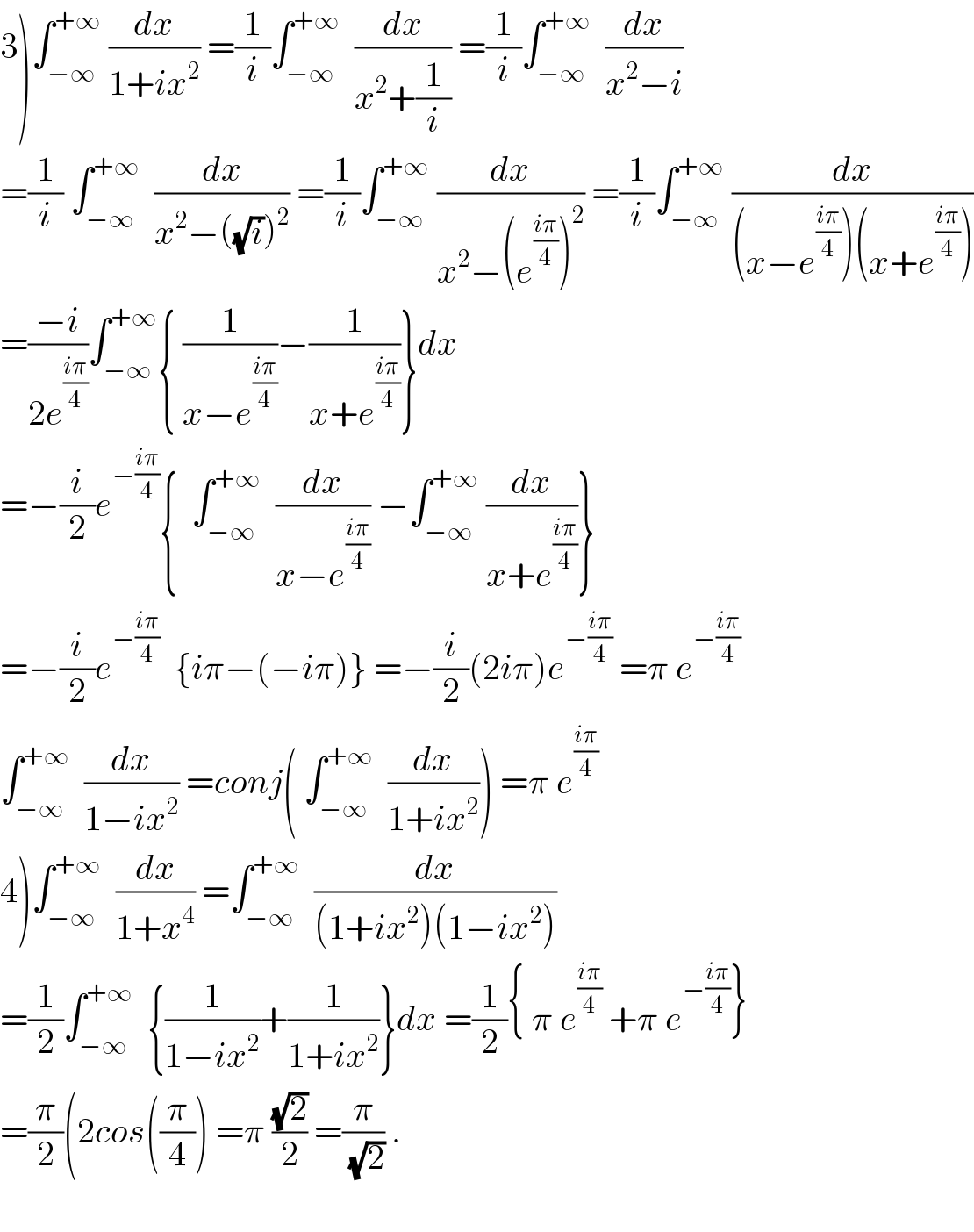
3)∫_(−∞) ^(+∞) (dx/(1+ix^2 )) =(1/i)∫_(−∞) ^(+∞) (dx/(x^2 +(1/i))) =(1/i)∫_(−∞) ^(+∞) (dx/(x^2 −i)) =(1/i) ∫_(−∞) ^(+∞) (dx/(x^2 −((√i))^2 )) =(1/i)∫_(−∞) ^(+∞) (dx/(x^2 −(e^((iπ)/4) )^2 )) =(1/i)∫_(−∞) ^(+∞) (dx/((x−e^((iπ)/4) )(x+e^((iπ)/4) ))) =((−i)/(2e^((iπ)/4) ))∫_(−∞) ^(+∞) { (1/(x−e^((iπ)/4) ))−(1/(x+e^((iπ)/4) ))}dx =−(i/2)e^(−((iπ)/4)) { ∫_(−∞) ^(+∞) (dx/(x−e^((iπ)/4) )) −∫_(−∞) ^(+∞) (dx/(x+e^((iπ)/4) ))} =−(i/2)e^(−((iπ)/4)) {iπ−(−iπ)} =−(i/2)(2iπ)e^(−((iπ)/4)) =π e^(−((iπ)/4)) ∫_(−∞) ^(+∞) (dx/(1−ix^2 )) =conj( ∫_(−∞) ^(+∞) (dx/(1+ix^2 ))) =π e^((iπ)/4) 4)∫_(−∞) ^(+∞) (dx/(1+x^4 )) =∫_(−∞) ^(+∞) (dx/((1+ix^2 )(1−ix^2 ))) =(1/2)∫_(−∞) ^(+∞) {(1/(1−ix^2 ))+(1/(1+ix^2 ))}dx =(1/2){ π e^((iπ)/4) +π e^(−((iπ)/4)) } =(π/2)(2cos((π/4)) =π ((√2)/2) =(π/( (√2))) .
$$\left.\mathrm{3}\right)\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\mathrm{1}+{ix}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{i}}\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{i}}}\:=\frac{\mathrm{1}}{{i}}\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} −{i}} \\ $$$$=\frac{\mathrm{1}}{{i}}\:\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} −\left(\sqrt{{i}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{i}}\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{2}} −\left({e}^{\frac{{i}\pi}{\mathrm{4}}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{i}}\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({x}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$$=\frac{−{i}}{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{4}}} }\int_{−\infty} ^{+\infty} \left\{\:\frac{\mathrm{1}}{{x}−{e}^{\frac{{i}\pi}{\mathrm{4}}} }−\frac{\mathrm{1}}{{x}+{e}^{\frac{{i}\pi}{\mathrm{4}}} }\right\}{dx} \\ $$$$=−\frac{{i}}{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \left\{\:\:\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}−{e}^{\frac{{i}\pi}{\mathrm{4}}} }\:−\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}+{e}^{\frac{{i}\pi}{\mathrm{4}}} }\right\} \\ $$$$=−\frac{{i}}{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:\left\{{i}\pi−\left(−{i}\pi\right)\right\}\:=−\frac{{i}}{\mathrm{2}}\left(\mathrm{2}{i}\pi\right){e}^{−\frac{{i}\pi}{\mathrm{4}}} \:=\pi\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\mathrm{1}−{ix}^{\mathrm{2}} }\:={conj}\left(\:\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\mathrm{1}+{ix}^{\mathrm{2}} }\right)\:=\pi\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \\ $$$$\left.\mathrm{4}\right)\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }\:=\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\left(\mathrm{1}+{ix}^{\mathrm{2}} \right)\left(\mathrm{1}−{ix}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\:\left\{\frac{\mathrm{1}}{\mathrm{1}−{ix}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}+{ix}^{\mathrm{2}} }\right\}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\pi\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:+\pi\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{4}}\right)\:=\pi\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:.\right. \\ $$$$ \\ $$
Commented by ~ À ® @ 237 ~ last updated on 05/Aug/19
Please check if there are some mistake : cause normally C=2[arctanx]_0 ^∞ =π
$${Please}\:{check}\:{if}\:{there}\:{are}\:{some}\:{mistake}\::\:{cause}\:{normally}\:{C}=\mathrm{2}\left[{arctanx}\right]_{\mathrm{0}} ^{\infty} =\pi \\ $$
Commented by mathmax by abdo last updated on 05/Aug/19
1) we have proved thst ∫_(−∞) ^(+∞) (dx/(x−a)) =iπ if im(a)>0 and −iπ if im(a)<0 so ∫_(−∞) ^(+∞) (dx/(1+ix)) =∫_(−∞) ^(+∞) (dx/(i(x+(1/i)))) =(1/i) ∫_(−∞) ^(+∞) (dx/(x−i)) =(1/i)(iπ) =π also ∫_(−∞) ^(+∞) (dx/(1−ix)) =(1/i)∫_(−∞) ^(+∞) (dx/((1/i)−x)) =−(1/i) ∫_(−∞) ^(+∞) (dx/(x−(1/i))) =−(1/i)∫_(−∞) ^(+∞) (dx/(x+i)) =−(1/i)(−iπ) =π 2)∫_(−∞) ^(+∞) (dx/(1+x^2 )) =∫_(−∞) ^(+∞) (dx/((x−i)(x+i))) =(1/(2i))∫_(−∞) ^(+∞) {(1/(x−i))−(1/(x+i))}dx =(1/(2i)){ ∫_(−∞) ^(+∞) (dx/(x−i)) −∫_(−∞) ^(+∞) (dx/(x+i))} =(1/(2i)){iπ −(−iπ)} =π
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{proved}\:{thst}\:\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}−{a}}\:={i}\pi\:{if}\:{im}\left({a}\right)>\mathrm{0}\:{and}\:−{i}\pi\:{if} \\ $$$${im}\left({a}\right)<\mathrm{0}\:\:{so}\:\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\mathrm{1}+{ix}}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{i}\left({x}+\frac{\mathrm{1}}{{i}}\right)}\:=\frac{\mathrm{1}}{{i}}\:\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}−{i}}\:=\frac{\mathrm{1}}{{i}}\left({i}\pi\right) \\ $$$$=\pi\:\:{also}\:\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\mathrm{1}−{ix}}\:=\frac{\mathrm{1}}{{i}}\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\frac{\mathrm{1}}{{i}}−{x}}\:=−\frac{\mathrm{1}}{{i}}\:\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}−\frac{\mathrm{1}}{{i}}} \\ $$$$=−\frac{\mathrm{1}}{{i}}\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}+{i}}\:=−\frac{\mathrm{1}}{{i}}\left(−{i}\pi\right)\:=\pi \\ $$$$\left.\mathrm{2}\right)\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}−{i}\right)\left({x}+{i}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{−\infty} ^{+\infty} \left\{\frac{\mathrm{1}}{{x}−{i}}−\frac{\mathrm{1}}{{x}+{i}}\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}−{i}}\:−\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}+{i}}\right\}\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{{i}\pi\:−\left(−{i}\pi\right)\right\}\:=\pi \\ $$

Pin