Question Number 74637 by mathmax by abdo last updated on 28/Nov/19
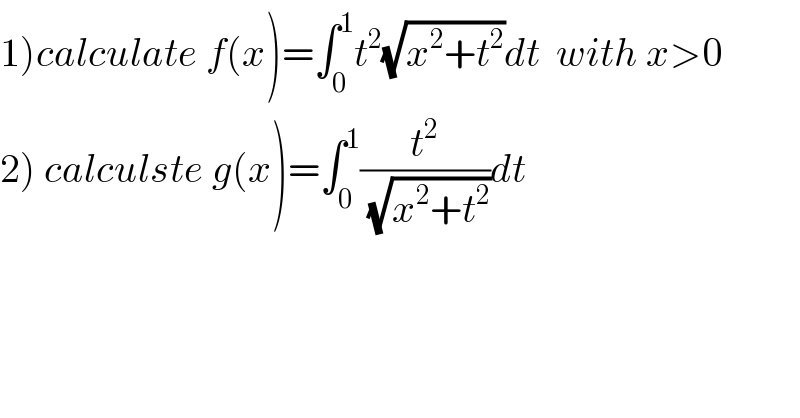
$$\left.\mathrm{1}\right){calculate}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +{t}^{\mathrm{2}} }{dt}\:\:{with}\:{x}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{calculste}\:{g}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} +{t}^{\mathrm{2}} }}{dt} \\ $$
Commented by mathmax by abdo last updated on 28/Nov/19
![1) we have f(x)=∫_0 ^1 t^2 (√(x^2 +t^2 ))dt ⇒f(x)=_(t=x sh(u)) ∫_0 ^(argsh((1/x))) x^2 sh^2 u(xch(u))xch(u)du = x^4 ∫_0 ^(ln((1/x)+(√(1+(1/x^2 ))))) sh^2 (u)ch^2 (u)du =(x^4 /4) ∫_0 ^(ln(((1+(√(x^2 +1)))/x))) sh^2 (2u) du =(x^4 /8) ∫_0 ^(ln(((1+(√(x^2 +1)))/x))) (ch(4u)−1))du =(x^4 /(32))[ sh(4u)]_0 ^(ln(((1+(√(x^2 +1)))/x))) −(x^4 /8)ln(((1+(√(x^2 +1)))/x)) =(x^4 /(64))[e^(4u) −e^(−4u) ]_0 ^(ln(((1+(√(x^2 +1)))/x))) −(x^4 /8)ln(((1+(√(x^2 +1)))/x)) =(x^4 /(64)){(((1+(√(x^2 +1)))/x))^4 −(((1+(√(x^2 +1)))/x))^(−4) }−(x^4 /8)ln(((1+(√(x^2 +1)))/x))](https://www.tinkutara.com/question/Q74681.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +{t}^{\mathrm{2}} }{dt}\:\:\Rightarrow{f}\left({x}\right)=_{{t}={x}\:{sh}\left({u}\right)} \:\int_{\mathrm{0}} ^{{argsh}\left(\frac{\mathrm{1}}{{x}}\right)} {x}^{\mathrm{2}} {sh}^{\mathrm{2}} {u}\left({xch}\left({u}\right)\right){xch}\left({u}\right){du} \\ $$$$=\:{x}^{\mathrm{4}} \int_{\mathrm{0}} ^{{ln}\left(\frac{\mathrm{1}}{{x}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\right)} \:\:\:{sh}^{\mathrm{2}} \left({u}\right){ch}^{\mathrm{2}} \left({u}\right){du} \\ $$$$\left.=\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\:\int_{\mathrm{0}} ^{{ln}\left(\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}\right)} {sh}^{\mathrm{2}} \left(\mathrm{2}{u}\right)\:{du}\:=\frac{{x}^{\mathrm{4}} }{\mathrm{8}}\:\int_{\mathrm{0}} ^{{ln}\left(\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}\right)} \left({ch}\left(\mathrm{4}{u}\right)−\mathrm{1}\right)\right){du} \\ $$$$=\frac{{x}^{\mathrm{4}} }{\mathrm{32}}\left[\:{sh}\left(\mathrm{4}{u}\right)\right]_{\mathrm{0}} ^{{ln}\left(\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}\right)} −\frac{{x}^{\mathrm{4}} }{\mathrm{8}}{ln}\left(\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}\right) \\ $$$$=\frac{{x}^{\mathrm{4}} }{\mathrm{64}}\left[{e}^{\mathrm{4}{u}} −{e}^{−\mathrm{4}{u}} \right]_{\mathrm{0}} ^{{ln}\left(\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}\right)} −\frac{{x}^{\mathrm{4}} }{\mathrm{8}}{ln}\left(\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}\right) \\ $$$$=\frac{{x}^{\mathrm{4}} }{\mathrm{64}}\left\{\left(\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}\right)^{\mathrm{4}} −\left(\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}\right)^{−\mathrm{4}} \right\}−\frac{{x}^{\mathrm{4}} }{\mathrm{8}}{ln}\left(\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}\right) \\ $$
Answered by MJS last updated on 28/Nov/19
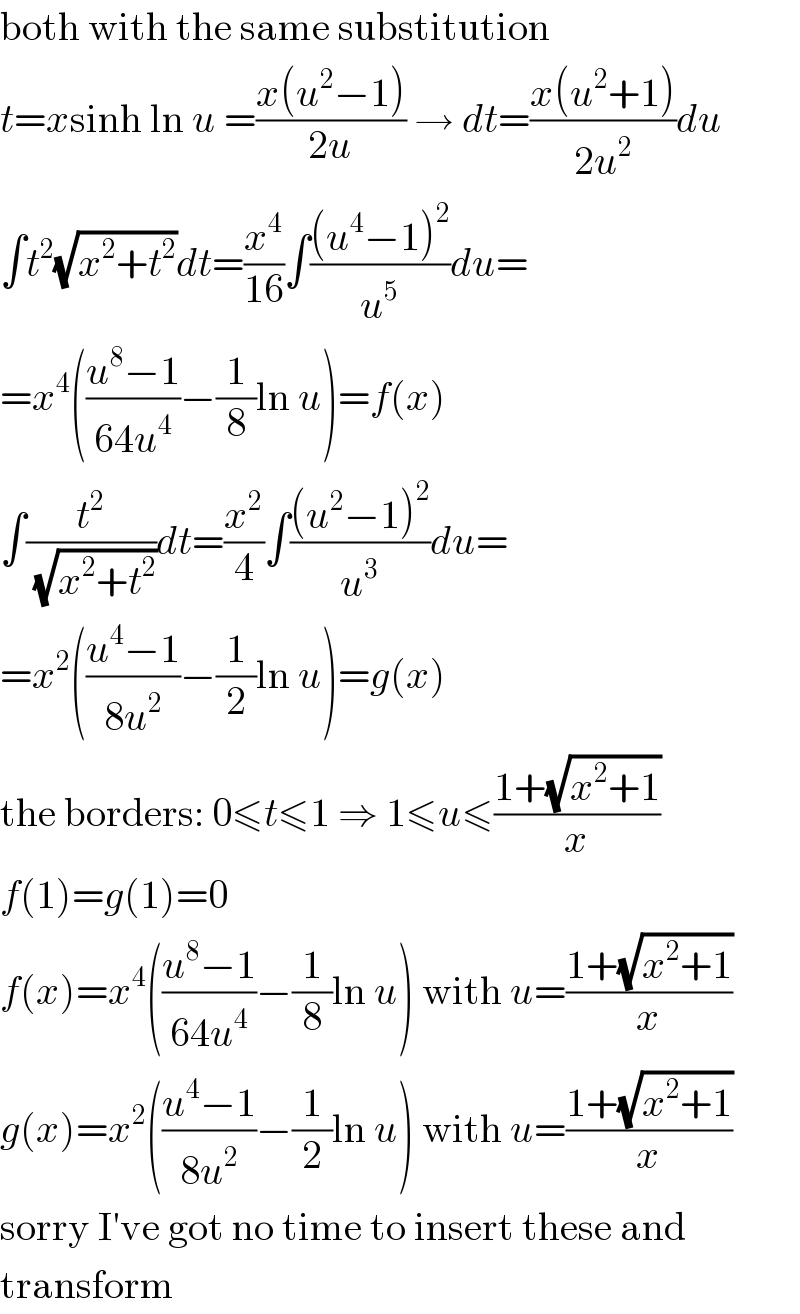
$$\mathrm{both}\:\mathrm{with}\:\mathrm{the}\:\mathrm{same}\:\mathrm{substitution} \\ $$$${t}={x}\mathrm{sinh}\:\mathrm{ln}\:{u}\:=\frac{{x}\left({u}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{2}{u}}\:\rightarrow\:{dt}=\frac{{x}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}{u}^{\mathrm{2}} }{du} \\ $$$$\int{t}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +{t}^{\mathrm{2}} }{dt}=\frac{{x}^{\mathrm{4}} }{\mathrm{16}}\int\frac{\left({u}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} }{{u}^{\mathrm{5}} }{du}= \\ $$$$={x}^{\mathrm{4}} \left(\frac{{u}^{\mathrm{8}} −\mathrm{1}}{\mathrm{64}{u}^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:{u}\right)={f}\left({x}\right) \\ $$$$\int\frac{{t}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} +{t}^{\mathrm{2}} }}{dt}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\int\frac{\left({u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{u}^{\mathrm{3}} }{du}= \\ $$$$={x}^{\mathrm{2}} \left(\frac{{u}^{\mathrm{4}} −\mathrm{1}}{\mathrm{8}{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{u}\right)={g}\left({x}\right) \\ $$$$\mathrm{the}\:\mathrm{borders}:\:\mathrm{0}\leqslant{t}\leqslant\mathrm{1}\:\Rightarrow\:\mathrm{1}\leqslant{u}\leqslant\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}} \\ $$$${f}\left(\mathrm{1}\right)={g}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${f}\left({x}\right)={x}^{\mathrm{4}} \left(\frac{{u}^{\mathrm{8}} −\mathrm{1}}{\mathrm{64}{u}^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:{u}\right)\:\mathrm{with}\:{u}=\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}} \\ $$$${g}\left({x}\right)={x}^{\mathrm{2}} \left(\frac{{u}^{\mathrm{4}} −\mathrm{1}}{\mathrm{8}{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{u}\right)\:\mathrm{with}\:{u}=\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}} \\ $$$$\mathrm{sorry}\:\mathrm{I}'\mathrm{ve}\:\mathrm{got}\:\mathrm{no}\:\mathrm{time}\:\mathrm{to}\:\mathrm{insert}\:\mathrm{these}\:\mathrm{and} \\ $$$$\mathrm{transform} \\ $$
