Question Number 74345 by mathmax by abdo last updated on 22/Nov/19
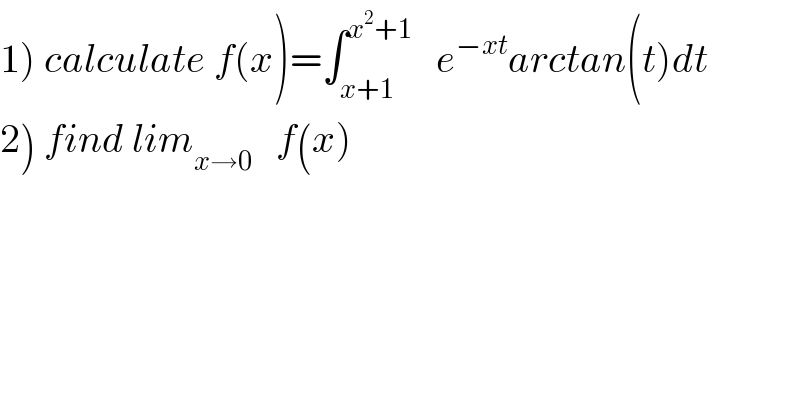
$$\left.\mathrm{1}\right)\:{calculate}\:{f}\left({x}\right)=\int_{{x}+\mathrm{1}} ^{{x}^{\mathrm{2}} +\mathrm{1}} \:\:\:{e}^{−{xt}} {arctan}\left({t}\right){dt} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:{f}\left({x}\right) \\ $$
Commented by mathmax by abdo last updated on 24/Nov/19
![1)f(x)=∫_(x+1) ^(x^2 +1) e^(−xt) arctan(t)dt ⇒f(x)=_(xt=u) (1/x)∫_(x^2 +x) ^(x^3 +x) e^(−u) arctan((u/x))du ⇒xf(x)=∫_(x^2 +x) ^(x^3 +x) e^(−u) arctan((u/x))dx =_(by parts) [−e^(−u) arctan((u/x))]_(x^2 +x) ^(x^3 +x) +∫_(x^2 +x) ^(x^3 +x) e^(−u) ×(1/(x(1+(u^2 /x^2 ))))du =e^(−(x^2 +x)) arctan(x+1)−e^(−(x^3 +x)) arctan(x^2 +1) +x ∫_(x^2 +x) ^(x^3 +x) (e^(−u) /(x^2 +u^2 ))du ⇒ f(x)=(1/x){ e^(−(x^2 +x)) arctan(x+1)−e^(−(x^3 +x)) arctan(x^2 +1)} +∫_(x^2 +x) ^(x^3 +x) (e^(−u) /(x^2 +u^2 ))du ...be continued...](https://www.tinkutara.com/question/Q74444.png)
$$\left.\mathrm{1}\right){f}\left({x}\right)=\int_{{x}+\mathrm{1}} ^{{x}^{\mathrm{2}} +\mathrm{1}} \:{e}^{−{xt}} \:{arctan}\left({t}\right){dt}\:\:\Rightarrow{f}\left({x}\right)=_{{xt}={u}} \:\frac{\mathrm{1}}{{x}}\int_{{x}^{\mathrm{2}} +{x}} ^{{x}^{\mathrm{3}} +{x}} \:{e}^{−{u}} \:{arctan}\left(\frac{{u}}{{x}}\right){du} \\ $$$$\Rightarrow{xf}\left({x}\right)=\int_{{x}^{\mathrm{2}} +{x}} ^{{x}^{\mathrm{3}} +{x}} \:{e}^{−{u}} \:{arctan}\left(\frac{{u}}{{x}}\right){dx}\:=_{{by}\:{parts}} \:\left[−{e}^{−{u}} \:{arctan}\left(\frac{{u}}{{x}}\right)\right]_{{x}^{\mathrm{2}} +{x}} ^{{x}^{\mathrm{3}} +{x}} \\ $$$$+\int_{{x}^{\mathrm{2}} +{x}} ^{{x}^{\mathrm{3}} +{x}} \:{e}^{−{u}} \:\:×\frac{\mathrm{1}}{{x}\left(\mathrm{1}+\frac{{u}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}{du} \\ $$$$={e}^{−\left({x}^{\mathrm{2}} +{x}\right)} \:{arctan}\left({x}+\mathrm{1}\right)−{e}^{−\left({x}^{\mathrm{3}} +{x}\right)} \:{arctan}\left({x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$+{x}\:\int_{{x}^{\mathrm{2}} +{x}} ^{{x}^{\mathrm{3}} +{x}} \:\:\:\frac{{e}^{−{u}} }{{x}^{\mathrm{2}} +{u}^{\mathrm{2}} }{du}\:\Rightarrow \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{x}}\left\{\:{e}^{−\left({x}^{\mathrm{2}} +{x}\right)} \:{arctan}\left({x}+\mathrm{1}\right)−{e}^{−\left({x}^{\mathrm{3}} +{x}\right)} \:{arctan}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\right\} \\ $$$$+\int_{{x}^{\mathrm{2}} +{x}} ^{{x}^{\mathrm{3}} +{x}} \:\:\frac{{e}^{−{u}} }{{x}^{\mathrm{2}} \:+{u}^{\mathrm{2}} }{du}\:\:…{be}\:{continued}… \\ $$
Commented by mathmax by abdo last updated on 24/Nov/19
![2) ∃ c_x ∈]x+1,x^2 +1[ /f(x)=arctanc_x ∫_(x+1) ^(x^2 +1) e^(−xt) dt =_(xt=u) arctan(c_x ) ∫_(x^2 +x) ^(x^3 +x) e^(−u) (du/x) =(1/x) arctan(c_x )[−e^(−u) ]_(x^2 +x) ^(x^3 +x) =arctan(c_x )×((e^(−(x^2 +x)) −e^(−(x^3 +x)) )/x) we have lim_(x→0) c_x =(π/4) also we have e^(−(x^2 +x)) ∼1−(x^2 +x) and e^(−(x^3 +x)) ∼1−(x^3 +x) ⇒ e^(−(x^2 +x)) −e^(−(x^3 +x)) =1−x^2 −x−1+x^3 +x =x^3 −x^2 ⇒ ((e^(−(x^2 +x)) −e^(−(x^3 +x)) )/x) ∼ x^2 −x →0 (x→0) ⇒lim_(x→0) f(x)=0](https://www.tinkutara.com/question/Q74445.png)
$$\left.\mathrm{2}\left.\right)\:\exists\:{c}_{{x}} \in\right]{x}+\mathrm{1},{x}^{\mathrm{2}} +\mathrm{1}\left[\:/{f}\left({x}\right)={arctanc}_{{x}} \:\int_{{x}+\mathrm{1}} ^{{x}^{\mathrm{2}} +\mathrm{1}} \:{e}^{−{xt}} \:{dt}\right. \\ $$$$=_{{xt}={u}} \:\:\:\:{arctan}\left({c}_{{x}} \right)\:\int_{{x}^{\mathrm{2}} +{x}} ^{{x}^{\mathrm{3}} \:+{x}} \:{e}^{−{u}} \frac{{du}}{{x}}\:=\frac{\mathrm{1}}{{x}}\:{arctan}\left({c}_{{x}} \right)\left[−{e}^{−{u}} \right]_{{x}^{\mathrm{2}} +{x}} ^{{x}^{\mathrm{3}} +{x}} \\ $$$$={arctan}\left({c}_{{x}} \right)×\frac{{e}^{−\left({x}^{\mathrm{2}} +{x}\right)} −{e}^{−\left({x}^{\mathrm{3}} +{x}\right)} }{{x}} \\ $$$${we}\:{have}\:{lim}_{{x}\rightarrow\mathrm{0}} {c}_{{x}} =\frac{\pi}{\mathrm{4}}\:\:{also}\:{we}\:{have}\:{e}^{−\left({x}^{\mathrm{2}} +{x}\right)} \sim\mathrm{1}−\left({x}^{\mathrm{2}} +{x}\right) \\ $$$${and}\:{e}^{−\left({x}^{\mathrm{3}} +{x}\right)} \sim\mathrm{1}−\left({x}^{\mathrm{3}} +{x}\right)\:\Rightarrow \\ $$$${e}^{−\left({x}^{\mathrm{2}} +{x}\right)} −{e}^{−\left({x}^{\mathrm{3}} +{x}\right)} =\mathrm{1}−{x}^{\mathrm{2}} −{x}−\mathrm{1}+{x}^{\mathrm{3}} +{x}\:={x}^{\mathrm{3}} −{x}^{\mathrm{2}} \:\Rightarrow \\ $$$$\frac{{e}^{−\left({x}^{\mathrm{2}} +{x}\right)} −{e}^{−\left({x}^{\mathrm{3}} +{x}\right)} }{{x}}\:\sim\:{x}^{\mathrm{2}} −{x}\:\rightarrow\mathrm{0}\:\:\left({x}\rightarrow\mathrm{0}\right)\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:{f}\left({x}\right)=\mathrm{0} \\ $$
