Question Number 74342 by mathmax by abdo last updated on 22/Nov/19
![1) calculate U_n =∫_0 ^∞ e^(−nx) [x]dx 2) find lim_(n→+∞) n U_n 3) determine nsture of the serie Σ U_n](https://www.tinkutara.com/question/Q74342.png)
$$\left.\mathrm{1}\right)\:{calculate}\:\:{U}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{nx}} \left[{x}\right]{dx} \\ $$$$\left.\mathrm{2}\right)\:{find}\:\:{lim}_{{n}\rightarrow+\infty} \:\:{n}\:{U}_{{n}} \\ $$$$\left.\mathrm{3}\right)\:{determine}\:{nsture}\:{of}\:{the}\:{serie}\:\Sigma\:{U}_{{n}} \\ $$
Commented by mathmax by abdo last updated on 23/Nov/19
![1) we have U_n =∫_0 ^∞ e^(−nx) [x]dx =Σ_(k=0) ^∞ ∫_k ^(k+1) e^(−nx) kdx =Σ_(k=0) ^∞ k [−(1/n) e^(−nx) ]_k ^(k+1) =(1/n)Σ_(k=0) ^∞ k{e^(−nk) −e^(−n(k+1)) } ⇒nU_n =Σ_(k=0) ^∞ k e^(−nk) −Σ_(k=0) ^∞ k e^(−n(k+1)) =Σ_(k=0) ^∞ k e^(−nk) −Σ_(k=1) ^∞ (k−1)e^(−nk) =Σ_(k=1) ^∞ k e^(−nk) −Σ_(k=1) ^∞ k e^(−nk) +Σ_(k=1) ^∞ e^(−nk) =Σ_(k=0) ^∞ (e^(−n) )^k −1 =(1/(1−e^(−n) )) −1 =((1−1+e^(−n) )/(1−e^(−n) )) ⇒nU_n =(e^(−n) /(1−e^(−n) )) =(1/(e^n −1)) ⇒ U_n =(1/(n(e^n −1))) (n>0) 2)we have U_n =(1/(n(e^n −1))) ⇒U_n ∼(1/(ne^n )) →0 ⇒lim_(n→+∞) U_n =0 3)U_n →0 and decrease so Σ U_n and ∫_1 ^(+∞) (dt/(te^t )) have the same nature and ∫_1 ^(+∞) (e^(−t) /t) dt converges ⇒Σ U_n converges.](https://www.tinkutara.com/question/Q74390.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{U}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{e}^{−{nx}} \left[{x}\right]{dx}\:=\sum_{{k}=\mathrm{0}} ^{\infty} \:\int_{{k}} ^{{k}+\mathrm{1}} \:{e}^{−{nx}} {kdx} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\infty} \:{k}\:\:\left[−\frac{\mathrm{1}}{{n}}\:{e}^{−{nx}} \right]_{{k}} ^{{k}+\mathrm{1}} =\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{0}} ^{\infty} \:{k}\left\{{e}^{−{nk}} −{e}^{−{n}\left({k}+\mathrm{1}\right)} \right\} \\ $$$$\Rightarrow{nU}_{{n}} =\sum_{{k}=\mathrm{0}} ^{\infty} \:{k}\:{e}^{−{nk}} \:−\sum_{{k}=\mathrm{0}} ^{\infty} \:{k}\:{e}^{−{n}\left({k}+\mathrm{1}\right)} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\infty} \:{k}\:{e}^{−{nk}} \:−\sum_{{k}=\mathrm{1}} ^{\infty} \:\left({k}−\mathrm{1}\right){e}^{−{nk}} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{\infty} \:{k}\:{e}^{−{nk}} −\sum_{{k}=\mathrm{1}} ^{\infty} \:{k}\:{e}^{−{nk}} \:+\sum_{{k}=\mathrm{1}} ^{\infty} \:{e}^{−{nk}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\infty} \:\left({e}^{−{n}} \right)^{{k}} −\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{1}−{e}^{−{n}} }\:−\mathrm{1}\:=\frac{\mathrm{1}−\mathrm{1}+{e}^{−{n}} }{\mathrm{1}−{e}^{−{n}} }\:\Rightarrow{nU}_{{n}} =\frac{{e}^{−{n}} }{\mathrm{1}−{e}^{−{n}} } \\ $$$$=\frac{\mathrm{1}}{{e}^{{n}} −\mathrm{1}}\:\Rightarrow\:{U}_{{n}} =\frac{\mathrm{1}}{{n}\left({e}^{{n}} −\mathrm{1}\right)}\:\:\:\left({n}>\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right){we}\:{have}\:{U}_{{n}} =\frac{\mathrm{1}}{{n}\left({e}^{{n}} −\mathrm{1}\right)}\:\Rightarrow{U}_{{n}} \sim\frac{\mathrm{1}}{{ne}^{{n}} }\:\rightarrow\mathrm{0}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} {U}_{{n}} =\mathrm{0} \\ $$$$\left.\mathrm{3}\right){U}_{{n}} \rightarrow\mathrm{0}\:{and}\:{decrease}\:{so}\:\Sigma\:{U}_{{n}} \:\:{and}\:\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dt}}{{te}^{{t}} }\:\:{have}\:{the}\:{same} \\ $$$${nature}\:\:\:{and}\:\int_{\mathrm{1}} ^{+\infty} \:\frac{{e}^{−{t}} }{{t}}\:{dt}\:\:\:{converges}\:\Rightarrow\Sigma\:{U}_{{n}} \:{converges}. \\ $$
Commented by mathmax by abdo last updated on 23/Nov/19
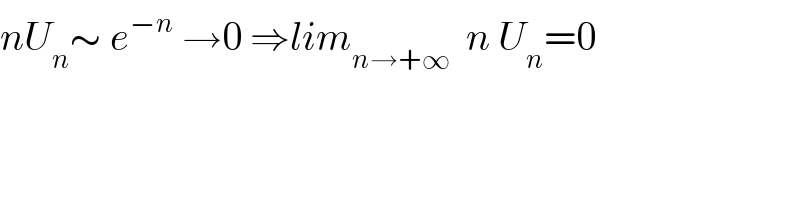
$${nU}_{{n}} \sim\:{e}^{−{n}} \:\rightarrow\mathrm{0}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:\:{n}\:{U}_{{n}} =\mathrm{0} \\ $$
Answered by mind is power last updated on 22/Nov/19
![U_n =Σ_(k=0) ^(+∞) ∫_k ^(k+1) e^(−nx) [x]dx =Σ_(k=0) ^(+∞) ∫_k ^(k+1) e^(−nx) .k=Σ_(k≥0) ke^(−nx) .−(1/n) =Σ−(k/n)(e^(−n(k+1)) −e^(−nk) ) =Σ_(k≥0) ((−ke^(−nk) (e^(−n) −1))/n)⇒nU_n =−(e^(−n) −1)(Σ_(k≥1) ke^(−nk) ) =−(e^(−n) −1).(e^(−n) +Σ_(k≥2) ke^(−nk) ) Σke^(−nk) ≤e^(−n) Σke^(−k) ∀n,k withe n≥2,k≥2 nk≥n+k ⇔n(k−1)−k≥0⇔(n−1)(k−1)≥1 clear ⇒e^(−nk) ≤e^(−n) .e^(−k) ⇒Σke^(−nk) ≤e^(−n) .(Σke^(−k) )→0 ⇒lim nU_n →0](https://www.tinkutara.com/question/Q74356.png)
$${U}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} {e}^{−{nx}} \left[{x}\right]{dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} {e}^{−{nx}} .{k}=\underset{{k}\geqslant\mathrm{0}} {\sum}{ke}^{−{nx}} .−\frac{\mathrm{1}}{{n}} \\ $$$$=\Sigma−\frac{{k}}{{n}}\left({e}^{−{n}\left({k}+\mathrm{1}\right)} −{e}^{−{nk}} \right) \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{−{ke}^{−{nk}} \left({e}^{−{n}} −\mathrm{1}\right)}{{n}}\Rightarrow{nU}_{{n}} =−\left({e}^{−{n}} −\mathrm{1}\right)\left(\underset{{k}\geqslant\mathrm{1}} {\sum}{ke}^{−{nk}} \right) \\ $$$$=−\left({e}^{−{n}} −\mathrm{1}\right).\left({e}^{−{n}} +\underset{{k}\geqslant\mathrm{2}} {\sum}{ke}^{−{nk}} \right) \\ $$$$\Sigma{ke}^{−{nk}} \leqslant{e}^{−{n}} \Sigma{ke}^{−{k}} \\ $$$$\forall{n},{k}\:\:\:{withe}\:{n}\geqslant\mathrm{2},{k}\geqslant\mathrm{2} \\ $$$${nk}\geqslant{n}+{k} \\ $$$$\Leftrightarrow{n}\left({k}−\mathrm{1}\right)−{k}\geqslant\mathrm{0}\Leftrightarrow\left({n}−\mathrm{1}\right)\left({k}−\mathrm{1}\right)\geqslant\mathrm{1}\:{clear} \\ $$$$\Rightarrow{e}^{−{nk}} \leqslant{e}^{−{n}} .{e}^{−{k}} \\ $$$$\Rightarrow\Sigma{ke}^{−{nk}} \leqslant{e}^{−{n}} .\left(\Sigma{ke}^{−{k}} \right)\rightarrow\mathrm{0} \\ $$$$\Rightarrow{lim}\:{nU}_{{n}} \rightarrow\mathrm{0} \\ $$$$ \\ $$
