Question Number 8419 by arinto27 last updated on 10/Oct/16

$$\left.\mathrm{1}\right)\:\mathrm{diket}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}−\mathrm{13},\:\mathrm{g}^{−\mathrm{1}} \left(\mathrm{x}\right)=\frac{\mathrm{x}+\mathrm{4}}{\mathrm{5}}\:\mathrm{dan}\:\mathrm{h}^{−\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{5x}+\mathrm{7} \\ $$$$\:\:\:\:\:\:\mathrm{nilai}\:\left(\mathrm{f}\:\mathrm{o}\:\left(\:\mathrm{g}\:\mathrm{o}\:\mathrm{h}\:\right)\right)^{−\mathrm{1}} \left(\mathrm{3}\right)=…? \\ $$$$\left.\mathrm{2}\right)\mathrm{diket}\:\mathrm{f}\left(\mathrm{x}\right)^{−\mathrm{1}} =\mathrm{4x}+\mathrm{5},\:\mathrm{g}\left(\mathrm{x}\right)=\frac{\mathrm{x}+\mathrm{4}}{\mathrm{5}}\:\mathrm{dan}\:\mathrm{h}^{−\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{x}−\mathrm{7} \\ $$$$\:\:\:\:\mathrm{nilai}\:\left(\:\mathrm{f}\:\mathrm{o}\:\mathrm{g}\:\mathrm{o}\:\mathrm{h}\:\right)^{−\mathrm{1}} \left(−\mathrm{2}\right)=….?? \\ $$$$\left.\mathrm{3}\right)\:\mathrm{jika}\:\mathrm{diket}\:\mathrm{invers}\:\mathrm{dari}\:\mathrm{fungsi}\:\mathrm{f}\:\mathrm{adalah}\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{3x}^{\mathrm{2}} +\mathrm{2} \\ $$$$\:\:\:\:\mathrm{dan}\:\mathrm{invers}\:\mathrm{dari}\:\mathrm{fungsi}\:\mathrm{g}\:\mathrm{adalah}\:\mathrm{g}^{−\mathrm{1}} \left(\mathrm{x}\right)=\sqrt{\mathrm{x}+\mathrm{1}} \\ $$$$\:\:\:\:×\:\geqslant−\mathrm{1}\:\mathrm{maka}\:\left(\:\mathrm{g}\:\mathrm{o}\:\mathrm{f}\:\right)^{−\mathrm{1}} \left(\mathrm{x}\right)=….? \\ $$$$\left.\mathrm{4}\right)\:\mathrm{jika}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}−\mathrm{3}\:\mathrm{dan}\:\mathrm{g}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{3x}+\mathrm{1}}\:\mathrm{utk}\:\mathrm{x}\neq−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\mathrm{maka}\:\left(\mathrm{g}\:\mathrm{o}\:\mathrm{f}\right)^{−\mathrm{1}} \left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)=….? \\ $$$$ \\ $$$$\mathrm{sebelumnya}\:\mathrm{saya}\:\mathrm{ucapkan}\:\mathrm{banyak}\:\mathrm{terima}\:\mathrm{kasih}… \\ $$
Answered by sandy_suhendra last updated on 10/Oct/16
![1) f(x)=2x−13 y = 2x−13 2x=y+13 x = ((y+13)/2) f(x)^(−1) = ((x+13)/2) (g o h)^(−1) (x)=(h^(−1) o g^(−1) )(x)=5(((x+4)/5))+7=x+11 [f o (g o h)]^(−1) (x)=[(g o h)^(−1) o f^(−1) ](x) =((x+13)/2)+11 [f o (g o h)]^(−1) (3) =((3+13)/2)+11=19](https://www.tinkutara.com/question/Q8422.png)
$$\left.\:\mathrm{1}\right)\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}−\mathrm{13} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{y}\:=\:\mathrm{2x}−\mathrm{13} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2x}=\mathrm{y}+\mathrm{13} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:=\:\frac{\mathrm{y}+\mathrm{13}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)^{−\mathrm{1}} =\:\frac{\mathrm{x}+\mathrm{13}}{\mathrm{2}} \\ $$$$\left(\mathrm{g}\:\mathrm{o}\:\mathrm{h}\right)^{−\mathrm{1}} \left(\mathrm{x}\right)=\left(\mathrm{h}^{−\mathrm{1}} \mathrm{o}\:\mathrm{g}^{−\mathrm{1}} \right)\left(\mathrm{x}\right)=\mathrm{5}\left(\frac{\mathrm{x}+\mathrm{4}}{\mathrm{5}}\right)+\mathrm{7}=\mathrm{x}+\mathrm{11} \\ $$$$\left[\mathrm{f}\:\mathrm{o}\:\left(\mathrm{g}\:\mathrm{o}\:\mathrm{h}\right)\right]^{−\mathrm{1}} \left(\mathrm{x}\right)=\left[\left(\mathrm{g}\:\mathrm{o}\:\mathrm{h}\right)^{−\mathrm{1}} \:\mathrm{o}\:\mathrm{f}^{−\mathrm{1}} \right]\left(\mathrm{x}\right)\:=\frac{\mathrm{x}+\mathrm{13}}{\mathrm{2}}+\mathrm{11} \\ $$$$\left[\mathrm{f}\:\mathrm{o}\:\left(\mathrm{g}\:\mathrm{o}\:\mathrm{h}\right)\right]^{−\mathrm{1}} \left(\mathrm{3}\right)\:=\frac{\mathrm{3}+\mathrm{13}}{\mathrm{2}}+\mathrm{11}=\mathrm{19} \\ $$
Answered by sandy_suhendra last updated on 10/Oct/16
![2) g(x)=((x+4)/5) y = ((x+4)/5) 5y=x+4 x=5y−4 g(x)^(−1) =5x−4 (f o g o h)^(−1) (−2) = (h^(−1) o g^(−1) o f^(−1) )(−2) f^(−1) (−2)=4(−2)+5=−3 (g^(−1) o f^(−1) )(−2)=g^(−1) [f^(−1) (−2)]=g^(−1) (−3)=5(−3)−4=−19 (h^(−1) o g^(−1) o f^(−1) )(−2)=h^(−1) [g^(−1) o f^(−1) (−2)] =h^(−1) (−19)=−19−7=−26](https://www.tinkutara.com/question/Q8423.png)
$$\left.\mathrm{2}\right)\:\mathrm{g}\left(\mathrm{x}\right)=\frac{\mathrm{x}+\mathrm{4}}{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{y}\:=\:\frac{\mathrm{x}+\mathrm{4}}{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{5y}=\mathrm{x}+\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\mathrm{5y}−\mathrm{4} \\ $$$$\:\:\:\mathrm{g}\left(\mathrm{x}\right)^{−\mathrm{1}} =\mathrm{5x}−\mathrm{4} \\ $$$$\left(\mathrm{f}\:\mathrm{o}\:\mathrm{g}\:\mathrm{o}\:\mathrm{h}\right)^{−\mathrm{1}} \left(−\mathrm{2}\right)\:=\:\left(\mathrm{h}^{−\mathrm{1}} \mathrm{o}\:\mathrm{g}^{−\mathrm{1}} \mathrm{o}\:\mathrm{f}^{−\mathrm{1}} \right)\left(−\mathrm{2}\right) \\ $$$$\mathrm{f}^{−\mathrm{1}} \left(−\mathrm{2}\right)=\mathrm{4}\left(−\mathrm{2}\right)+\mathrm{5}=−\mathrm{3} \\ $$$$\left(\mathrm{g}^{−\mathrm{1}} \mathrm{o}\:\mathrm{f}^{−\mathrm{1}} \right)\left(−\mathrm{2}\right)=\mathrm{g}^{−\mathrm{1}} \left[\mathrm{f}^{−\mathrm{1}} \left(−\mathrm{2}\right)\right]=\mathrm{g}^{−\mathrm{1}} \left(−\mathrm{3}\right)=\mathrm{5}\left(−\mathrm{3}\right)−\mathrm{4}=−\mathrm{19} \\ $$$$\left(\mathrm{h}^{−\mathrm{1}} \mathrm{o}\:\mathrm{g}^{−\mathrm{1}} \mathrm{o}\:\mathrm{f}^{−\mathrm{1}} \right)\left(−\mathrm{2}\right)=\mathrm{h}^{−\mathrm{1}} \left[\mathrm{g}^{−\mathrm{1}} \mathrm{o}\:\mathrm{f}^{−\mathrm{1}} \left(−\mathrm{2}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{h}^{−\mathrm{1}} \left(−\mathrm{19}\right)=−\mathrm{19}−\mathrm{7}=−\mathrm{26} \\ $$
Answered by sandy_suhendra last updated on 10/Oct/16
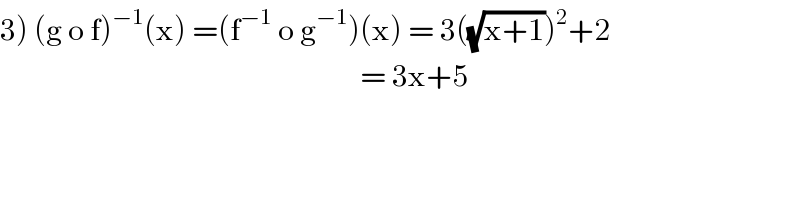
$$\left.\mathrm{3}\right)\:\left(\mathrm{g}\:\mathrm{o}\:\mathrm{f}\right)^{−\mathrm{1}} \left(\mathrm{x}\right)\:=\left(\mathrm{f}^{−\mathrm{1}} \:\mathrm{o}\:\mathrm{g}^{−\mathrm{1}} \right)\left(\mathrm{x}\right)\:=\:\mathrm{3}\left(\sqrt{\mathrm{x}+\mathrm{1}}\right)^{\mathrm{2}} +\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{3x}+\mathrm{5} \\ $$
Answered by sandy_suhendra last updated on 10/Oct/16
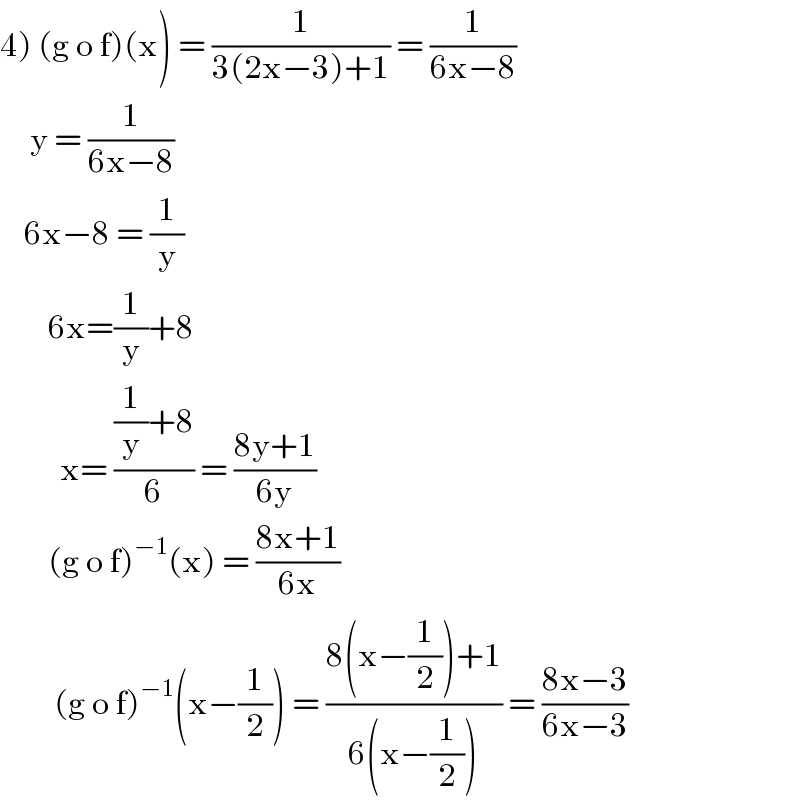
$$\left.\mathrm{4}\right)\:\left(\mathrm{g}\:\mathrm{o}\:\mathrm{f}\right)\left(\mathrm{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{2x}−\mathrm{3}\right)+\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{6x}−\mathrm{8}} \\ $$$$\:\:\:\:\:\mathrm{y}\:=\:\frac{\mathrm{1}}{\mathrm{6x}−\mathrm{8}} \\ $$$$\:\:\:\:\mathrm{6x}−\mathrm{8}\:=\:\frac{\mathrm{1}}{\mathrm{y}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{6x}=\frac{\mathrm{1}}{\mathrm{y}}+\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\:\frac{\frac{\mathrm{1}}{\mathrm{y}}+\mathrm{8}}{\mathrm{6}}\:=\:\frac{\mathrm{8y}+\mathrm{1}}{\mathrm{6y}} \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{g}\:\mathrm{o}\:\mathrm{f}\right)^{−\mathrm{1}} \left(\mathrm{x}\right)\:=\:\frac{\mathrm{8x}+\mathrm{1}}{\mathrm{6x}} \\ $$$$\:\:\:\:\:\:\:\:\:\left(\mathrm{g}\:\mathrm{o}\:\mathrm{f}\right)^{−\mathrm{1}} \left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{8}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{1}}{\mathrm{6}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{8x}−\mathrm{3}}{\mathrm{6x}−\mathrm{3}} \\ $$
