Menu Close

1-dx-1-sin-x-cos-x-2-0-x-x-3-1-dx-3-0-1-x-3-2-1-dx-

Tinku Tara
Pin




Question Number 131247 by bramlexs22 last updated on 03/Feb/21
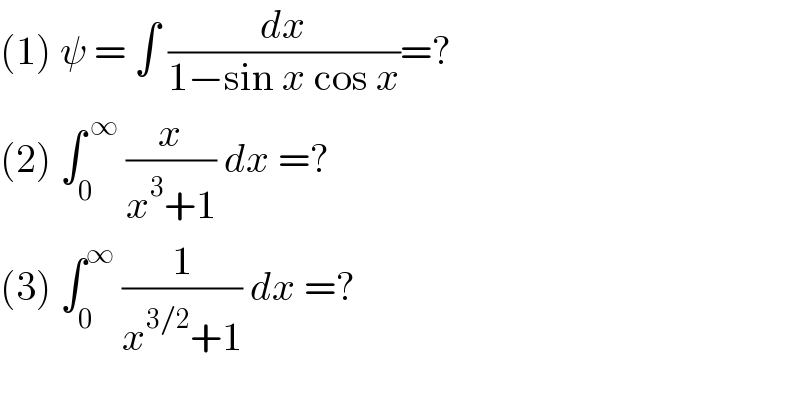
(1) ψ = ∫ (dx/(1−sin x cos x))=? (2) ∫_0 ^( ∞) (x/(x^3 +1)) dx =? (3) ∫_0 ^∞ (1/(x^(3/2) +1)) dx =?
$$\left(\mathrm{1}\right)\:\psi\:=\:\int\:\frac{{dx}}{\mathrm{1}−\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}=? \\ $$$$\left(\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{{x}}{{x}^{\mathrm{3}} +\mathrm{1}}\:{dx}\:=? \\ $$$$\left(\mathrm{3}\right)\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{x}^{\mathrm{3}/\mathrm{2}} +\mathrm{1}}\:{dx}\:=?\: \\ $$
Answered by liberty last updated on 03/Feb/21
Evaluate ∫_0 ^( ∞) (x/(x^3 +1)) dx. (2) L = ∫_0 ^( ∞) (x/(x^3 +1)) dx ; replace x with (1/x) L=∫_0 ^( ∞) ((1/x)/((1/x^3 )+1)) .(−(dx/x^2 )) = ∫_0 ^( ∞) (dx/(1+x^3 )) now we find that : 2L=∫_0 ^( ∞) ((x+1)/(x^3 +1)) dx 2L = ∫_0 ^( ∞) (1/(x^2 −x+1)) dx ; L=(1/2)∫_0 ^( ∞) (dx/((x−(1/2))^2 +(((√3)/2))^2 )) L= (1/2).(2/( (√3))) [tan^(−1) (((x−(1/2))/((√3)/2)))]_0 ^∞ = (1/( (√3))) [ tan^(−1) (((2x−1)/( (√3)))) ]_0 ^∞ L= (1/( (√3))) ((π/2)−(−(π/6)))= ((2π(√3))/9).
$$\:\:\:\:\:\:\:\:\mathrm{Evaluate}\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}}{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}\:\mathrm{dx}. \\ $$$$\left(\mathrm{2}\right)\:\mathrm{L}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}}{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}\:\mathrm{dx}\:;\:\mathrm{replace}\:\mathrm{x}\:\mathrm{with}\:\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\mathrm{L}=\int_{\mathrm{0}} ^{\:\infty} \frac{\frac{\mathrm{1}}{\mathrm{x}}}{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }+\mathrm{1}}\:.\left(−\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} }\right)\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\: \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{find}\:\mathrm{that}\::\:\mathrm{2L}=\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}\:\mathrm{dx}\: \\ $$$$\mathrm{2L}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\:\mathrm{dx}\:;\:\mathrm{L}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{L}=\:\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{\infty} =\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\left[\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:\right]_{\mathrm{0}} ^{\infty} \\ $$$$\mathrm{L}=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\left(\frac{\pi}{\mathrm{2}}−\left(−\frac{\pi}{\mathrm{6}}\right)\right)=\:\frac{\mathrm{2}\pi\sqrt{\mathrm{3}}}{\mathrm{9}}. \\ $$$$ \\ $$
Answered by liberty last updated on 03/Feb/21
Solve ψ = ∫ (dx/(1−sin x cos x)) (1) ψ=∫ (dx/(1−sin x cos x)) = ∫ ((sec^2 x)/(sec^2 x−tan x)) dx ψ=∫ ((d(tan x))/(tan^2 x−tan x+1)) ; [ change variable t=tan x ] ψ=∫ (dt/(t^2 −t+1)) = ∫ (dt/((t−(1/2))^2 +(((√3)/2))^2 )) ψ= (2/( (√3))) arctan (((t−(1/2))/((√3)/2)))+c ψ=(2/( (√3))) arctan (((2t−1)/( (√3)))) + c = (2/( (√3))) arctan (((2tan x−1)/( (√3))))+c ψ= ((2 arctan (((2tan x−1)/( (√3)))))/( (√3))) + c
$$\:\:\:\mathrm{Solve}\:\psi\:=\:\int\:\frac{\mathrm{dx}}{\mathrm{1}−\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}\: \\ $$$$\left(\mathrm{1}\right)\:\psi=\int\:\frac{\mathrm{dx}}{\mathrm{1}−\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}\:=\:\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}−\mathrm{tan}\:\mathrm{x}}\:\mathrm{dx} \\ $$$$\psi=\int\:\frac{\mathrm{d}\left(\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{tan}\:\mathrm{x}+\mathrm{1}}\:;\:\left[\:\mathrm{change}\:\mathrm{variable}\:\mathrm{t}=\mathrm{tan}\:\mathrm{x}\:\right] \\ $$$$\psi=\int\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}}\:=\:\int\:\frac{\mathrm{dt}}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\psi=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\mathrm{arctan}\:\left(\frac{\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)+\mathrm{c}\: \\ $$$$\psi=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\mathrm{arctan}\:\left(\frac{\mathrm{2t}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+\:\mathrm{c}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\mathrm{arctan}\:\left(\frac{\mathrm{2tan}\:\mathrm{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{c}\: \\ $$$$\psi=\:\frac{\mathrm{2}\:\mathrm{arctan}\:\left(\frac{\mathrm{2tan}\:\mathrm{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)}{\:\sqrt{\mathrm{3}}}\:+\:\mathrm{c}\: \\ $$
Commented by malwan last updated on 03/Feb/21
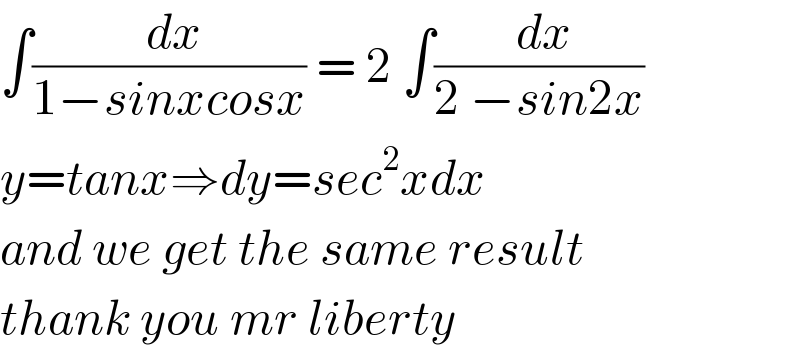
∫(( dx)/(1−sinxcosx)) = 2 ∫(( dx)/(2 −sin2x)) y=tanx⇒dy=sec^2 xdx and we get the same result thank you mr liberty
$$\int\frac{\:{dx}}{\mathrm{1}−{sinxcosx}}\:=\:\mathrm{2}\:\int\frac{\:{dx}}{\mathrm{2}\:−{sin}\mathrm{2}{x}} \\ $$$${y}={tanx}\Rightarrow{dy}={sec}^{\mathrm{2}} {xdx} \\ $$$${and}\:{we}\:{get}\:{the}\:{same}\:{result} \\ $$$${thank}\:{you}\:{mr}\:{liberty} \\ $$
Answered by liberty last updated on 03/Feb/21
(3) we want to evaluate η = ∫_0 ^( ∞) (dx/(x^(3/2) +1)). by rationalizing replace x^(1/2) by t or x=t^2 η=2∫_0 ^∞ (t/(t^3 +1)) dt ; where ∫_0 ^( ∞) (x/(x^3 +1))dx = ((2π(√3))/9) ( see the solution in part (2)) Hence we find η = ∫_( 0) ^( ∞) (dx/(x^(3/2) +1))= 2×(((2π(√3))/9))=((4π(√3))/9)
$$\:\left(\mathrm{3}\right)\:\mathrm{we}\:\mathrm{want}\:\mathrm{to}\:\mathrm{evaluate}\:\eta\:=\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}/\mathrm{2}} +\mathrm{1}}. \\ $$$$\:\mathrm{by}\:\mathrm{rationalizing}\:\mathrm{replace}\:\mathrm{x}^{\mathrm{1}/\mathrm{2}} \:\mathrm{by}\:\mathrm{t}\:\mathrm{or}\:\mathrm{x}=\mathrm{t}^{\mathrm{2}} \\ $$$$\:\eta=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}}{\mathrm{t}^{\mathrm{3}} +\mathrm{1}}\:\mathrm{dt}\:;\:\mathrm{where}\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}\mathrm{dx}\:=\:\frac{\mathrm{2}\pi\sqrt{\mathrm{3}}}{\mathrm{9}} \\ $$$$\:\left(\:\mathrm{see}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{in}\:\mathrm{part}\:\left(\mathrm{2}\right)\right) \\ $$$$\mathrm{Hence}\:\mathrm{we}\:\mathrm{find}\:\eta\:=\:\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}/\mathrm{2}} +\mathrm{1}}=\:\mathrm{2}×\left(\frac{\mathrm{2}\pi\sqrt{\mathrm{3}}}{\mathrm{9}}\right)=\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{9}} \\ $$
Answered by Ar Brandon last updated on 03/Feb/21
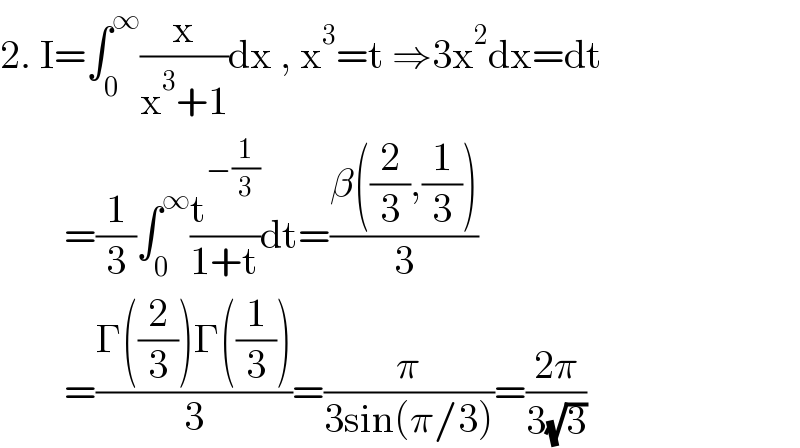
2. I=∫_0 ^∞ (x/(x^3 +1))dx , x^3 =t ⇒3x^2 dx=dt =(1/3)∫_0 ^∞ (t^(−(1/3)) /(1+t))dt=((β((2/3),(1/3)))/3) =((Γ((2/3))Γ((1/3)))/3)=(π/(3sin(π/3)))=((2π)/(3(√3)))
$$\mathrm{2}.\:\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}}{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}\mathrm{dx}\:,\:\mathrm{x}^{\mathrm{3}} =\mathrm{t}\:\Rightarrow\mathrm{3x}^{\mathrm{2}} \mathrm{dx}=\mathrm{dt} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}=\frac{\beta\left(\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{1}}{\mathrm{3}}\right)}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\mathrm{3}}=\frac{\pi}{\mathrm{3sin}\left(\pi/\mathrm{3}\right)}=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Commented by Engr_Jidda last updated on 03/Feb/21
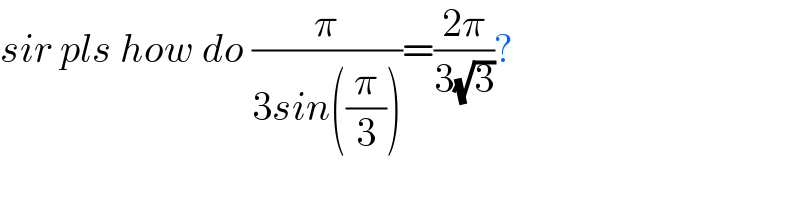
sir pls how do (π/(3sin((π/3))))=((2π)/(3(√3)))?
$${sir}\:{pls}\:{how}\:{do}\:\frac{\pi}{\mathrm{3}{sin}\left(\frac{\pi}{\mathrm{3}}\right)}=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}? \\ $$
Commented by malwan last updated on 03/Feb/21
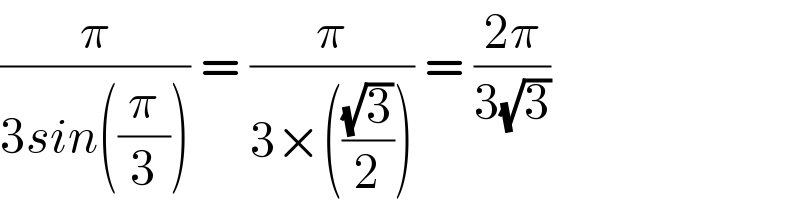
(π/(3sin((π/3)))) = (π/(3×(((√3)/2)))) = ((2π)/(3(√3)))
$$\frac{\pi}{\mathrm{3}{sin}\left(\frac{\pi}{\mathrm{3}}\right)}\:=\:\frac{\pi}{\mathrm{3}×\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Commented by Engr_Jidda last updated on 04/Feb/21
oh yeah, thanks
$${oh}\:{yeah},\:{thanks} \\ $$
Answered by Dwaipayan Shikari last updated on 03/Feb/21
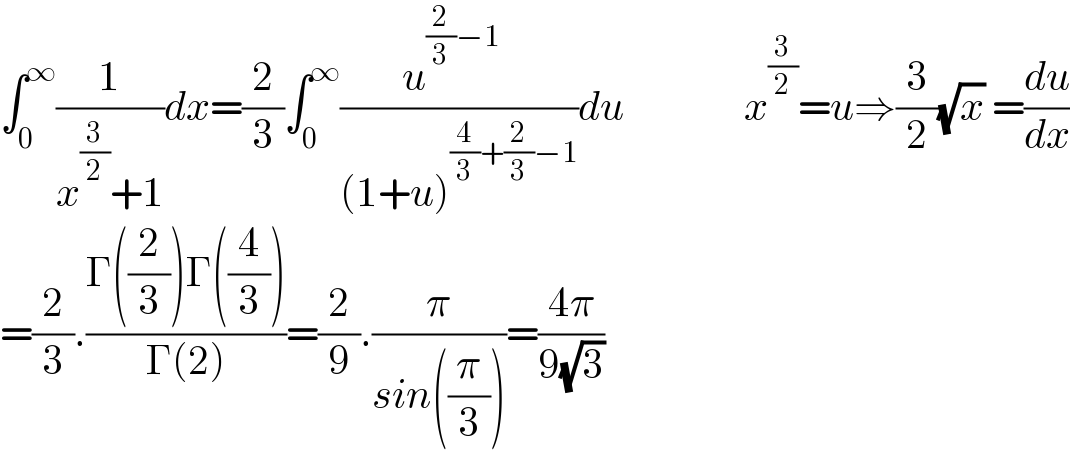
∫_0 ^∞ (1/(x^(3/2) +1))dx=(2/3)∫_0 ^∞ ((u^((2/3)−1) )/((1+u)^((4/3)+(2/3)−1) ))du x^(3/2) =u⇒(3/2)(√x) =(du/dx) =(2/3).((Γ((2/3))Γ((4/3)))/(Γ(2)))=(2/9).(π/(sin((π/3))))=((4π)/(9(√3)))
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{1}}{dx}=\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{1}} \:\:}{\left(\mathrm{1}+{u}\right)^{\frac{\mathrm{4}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{1}} }{du}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\frac{\mathrm{3}}{\mathrm{2}}} ={u}\Rightarrow\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{x}}\:=\frac{{du}}{{dx}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}.\frac{\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{4}}{\mathrm{3}}\right)}{\Gamma\left(\mathrm{2}\right)}=\frac{\mathrm{2}}{\mathrm{9}}.\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{3}}\right)}=\frac{\mathrm{4}\pi}{\mathrm{9}\sqrt{\mathrm{3}}} \\ $$
Answered by mathmax by abdo last updated on 03/Feb/21
1) Φ=∫ (dx/(1−sinx cosx)) ⇒Φ =∫ (dx/(1−((sin(2x))/2)))=2∫ (dx/(2−sin(2x))) =_(2x=t) ∫ (dt/(2−sint)) =_(tan((t/2))=y) ∫ ((2dy)/((1+y^2 )(2−((2y)/(1+y^2 ))))) =∫ ((2dy)/(2+2y^2 −2y)) =∫ (dy/(y^2 −y+1)) =∫ (dy/((y−(1/2))^2 +(3/4))) =_(y−(1/2)=((√3)/2)u) (4/3) ∫ (1/(u^(2 ) +1))((√3)/2)du =(1/( (√3)))arctanu +C =(1/( (√3)))arctan(((2y−1)/( (√3)))) +C =(1/( (√3)))arctan((1/( (√3)))(2tan(x)−1) +C
$$\left.\mathrm{1}\right)\:\Phi=\int\:\:\frac{\mathrm{dx}}{\mathrm{1}−\mathrm{sinx}\:\mathrm{cosx}}\:\Rightarrow\Phi\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{1}−\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}}}=\mathrm{2}\int\:\frac{\mathrm{dx}}{\mathrm{2}−\mathrm{sin}\left(\mathrm{2x}\right)} \\ $$$$=_{\mathrm{2x}=\mathrm{t}} \:\:\:\int\:\:\frac{\mathrm{dt}}{\mathrm{2}−\mathrm{sint}}\:=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{y}} \:\:\:\:\:\int\:\:\:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\left(\mathrm{2}−\frac{\mathrm{2y}}{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }\right)} \\ $$$$=\int\:\:\frac{\mathrm{2dy}}{\mathrm{2}+\mathrm{2y}^{\mathrm{2}} −\mathrm{2y}}\:=\int\:\:\frac{\mathrm{dy}}{\mathrm{y}^{\mathrm{2}} −\mathrm{y}+\mathrm{1}}\:=\int\:\frac{\mathrm{dy}}{\left(\mathrm{y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=_{\mathrm{y}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{u}} \:\:\:\:\:\frac{\mathrm{4}}{\mathrm{3}}\:\int\:\:\:\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}\:} +\mathrm{1}}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{du}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{arctanu}\:+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{2y}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+\mathrm{C}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{2tan}\left(\mathrm{x}\right)−\mathrm{1}\right)\:+\mathrm{C}\right. \\ $$
Answered by mathmax by abdo last updated on 03/Feb/21
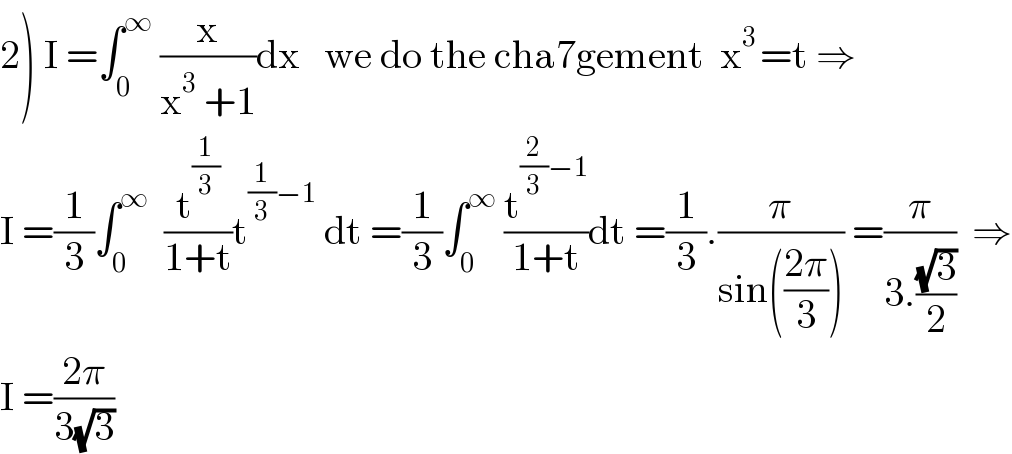
2) I =∫_0 ^∞ (x/(x^3 +1))dx we do the cha7gement x^(3 ) =t ⇒ I =(1/3)∫_0 ^∞ (t^(1/3) /(1+t))t^((1/3)−1) dt =(1/3)∫_0 ^∞ (t^((2/3)−1) /(1+t))dt =(1/3).(π/(sin(((2π)/3)))) =(π/(3.((√3)/2))) ⇒ I =((2π)/(3(√3)))
$$\left.\mathrm{2}\right)\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{3}} \:+\mathrm{1}}\mathrm{dx}\:\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{cha7gement}\:\:\mathrm{x}^{\mathrm{3}\:} =\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{1}+\mathrm{t}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{3}}.\frac{\pi}{\mathrm{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)}\:=\frac{\pi}{\mathrm{3}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Answered by mathmax by abdo last updated on 03/Feb/21
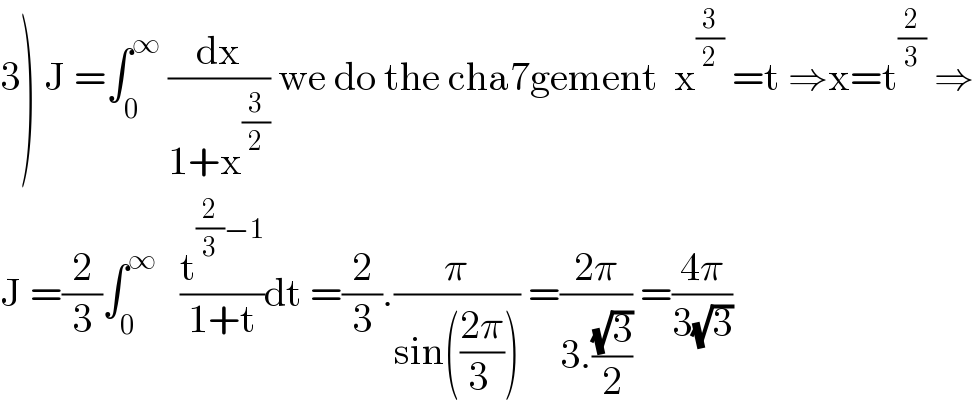
3) J =∫_0 ^∞ (dx/(1+x^(3/2) )) we do the cha7gement x^(3/2) =t ⇒x=t^(2/3) ⇒ J =(2/3)∫_0 ^∞ (t^((2/3)−1) /(1+t))dt =(2/3).(π/(sin(((2π)/(3 ))))) =((2π)/(3.((√3)/2))) =((4π)/(3(√3)))
$$\left.\mathrm{3}\right)\:\mathrm{J}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{cha7gement}\:\:\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \:=\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{t}^{\frac{\mathrm{2}}{\mathrm{3}}} \:\Rightarrow \\ $$$$\mathrm{J}\:=\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{t}^{\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\frac{\mathrm{2}}{\mathrm{3}}.\frac{\pi}{\mathrm{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}\:}\right)}\:=\frac{\mathrm{2}\pi}{\mathrm{3}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$

Pin