Question Number 310 by 123456 last updated on 25/Jan/15
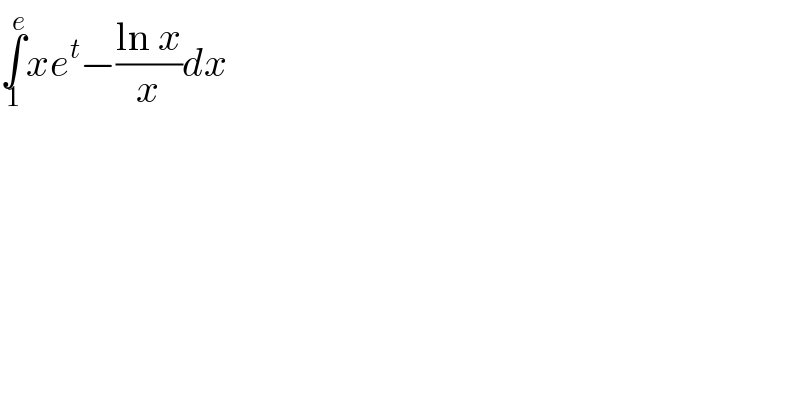
$$\underset{\mathrm{1}} {\overset{{e}} {\int}}{xe}^{{t}} −\frac{\mathrm{ln}\:{x}}{{x}}{dx} \\ $$
Answered by prakash jain last updated on 20/Dec/14
![∫xe^t dx−∫((ln x)/x)dx =[(x^2 /2)e^t −(((ln x)^2 )/2)]_1 ^e =[((e^2 e^t )/2)−(1/2)−((e^t /2)−0)] =(1/2)(e^(t+2) −e^t −1)](https://www.tinkutara.com/question/Q311.png)
$$\int{xe}^{{t}} {dx}−\int\frac{\mathrm{ln}\:{x}}{{x}}{dx} \\ $$$$=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{e}^{{t}} −\frac{\left(\mathrm{ln}\:{x}\right)^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{1}} ^{{e}} =\left[\frac{{e}^{\mathrm{2}} {e}^{{t}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}−\left(\frac{{e}^{{t}} }{\mathrm{2}}−\mathrm{0}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{t}+\mathrm{2}} −{e}^{{t}} −\mathrm{1}\right) \\ $$
