Question Number 77126 by peter frank last updated on 03/Jan/20
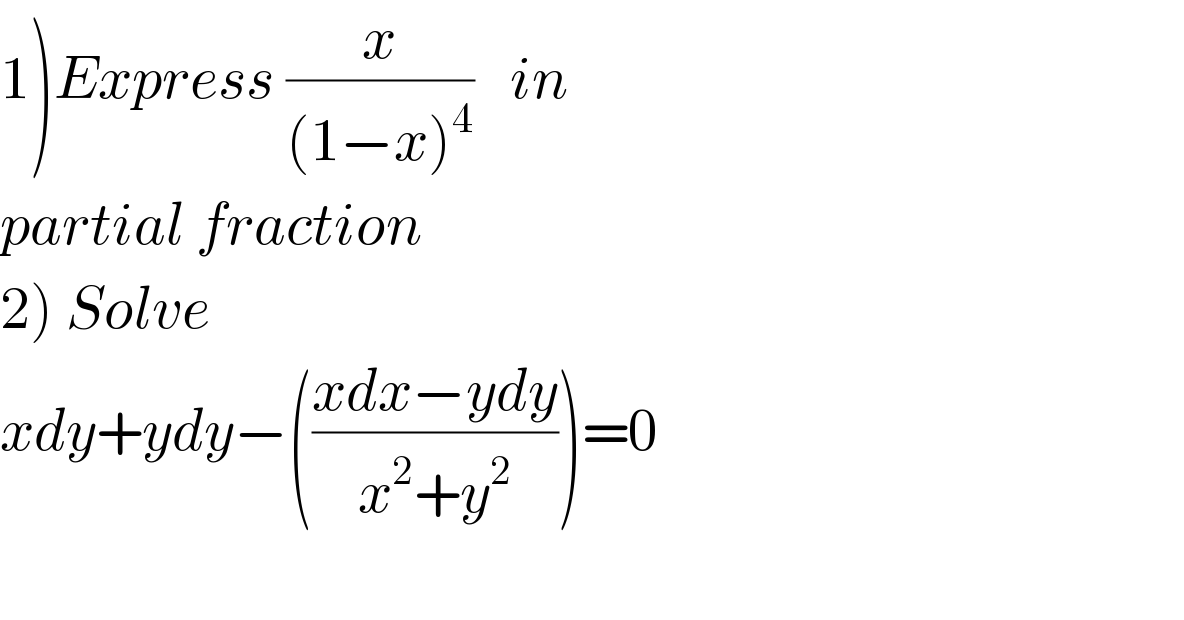
$$\left.\mathrm{1}\right){Express}\:\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }\:\:\:{in} \\ $$$${partial}\:{fraction} \\ $$$$\left.\mathrm{2}\right)\:{Solve} \\ $$$${xdy}+{ydy}−\left(\frac{{xdx}−{ydy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$ \\ $$
Answered by jagoll last updated on 03/Jan/20
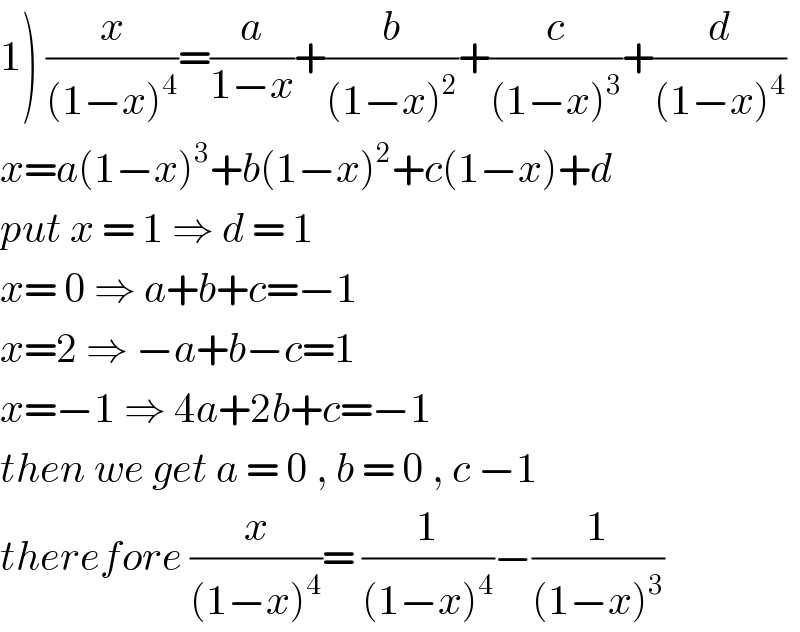
$$\left.\mathrm{1}\right)\:\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }=\frac{{a}}{\mathrm{1}−{x}}+\frac{{b}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{{c}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }+\frac{{d}}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} } \\ $$$${x}={a}\left(\mathrm{1}−{x}\right)^{\mathrm{3}} +{b}\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +{c}\left(\mathrm{1}−{x}\right)+{d} \\ $$$${put}\:{x}\:=\:\mathrm{1}\:\Rightarrow\:{d}\:=\:\mathrm{1} \\ $$$${x}=\:\mathrm{0}\:\Rightarrow\:{a}+{b}+{c}=−\mathrm{1} \\ $$$${x}=\mathrm{2}\:\Rightarrow\:−{a}+{b}−{c}=\mathrm{1} \\ $$$${x}=−\mathrm{1}\:\Rightarrow\:\mathrm{4}{a}+\mathrm{2}{b}+{c}=−\mathrm{1} \\ $$$${then}\:{we}\:{get}\:{a}\:=\:\mathrm{0}\:,\:{b}\:=\:\mathrm{0}\:,\:{c}\:−\mathrm{1} \\ $$$${therefore}\:\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }=\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }−\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$
Commented by peter frank last updated on 03/Jan/20

$${thank}\:{you} \\ $$
