Question Number 67057 by Tony Lin last updated on 22/Aug/19
![(1)find ∩_(n=1) ^∞ [0, (1/n)) (2)find ∪_(n=2) ^∞ [(1/n), 1−(1/n)]](https://www.tinkutara.com/question/Q67057.png)
$$\left(\mathrm{1}\right){find}\:\cap_{{n}=\mathrm{1}} ^{\infty} \left[\mathrm{0},\:\frac{\mathrm{1}}{{n}}\right) \\ $$$$\left(\mathrm{2}\right){find}\:\cup_{{n}=\mathrm{2}} ^{\infty} \left[\frac{\mathrm{1}}{{n}},\:\mathrm{1}−\frac{\mathrm{1}}{{n}}\right] \\ $$
Answered by Kunal12588 last updated on 22/Aug/19
![(1)=[0,1]∩[0,(1/2))∩[0,(1/3))∩...∞ terms = {0} (2)=[(1/2),(1/2)]∪[(1/3),(2/3)]∪[(1/4),(3/4)]∪...∪[0,1]=[0,1] are they correct i don′t have any experience of solving these type of questions. don′t even know meaning of ∪_(n=1) ^∞](https://www.tinkutara.com/question/Q67065.png)
$$\left(\mathrm{1}\right)=\left[\mathrm{0},\mathrm{1}\right]\cap\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right)\cap\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{3}}\right)\cap…\infty\:{terms}\:=\:\left\{\mathrm{0}\right\} \\ $$$$\left(\mathrm{2}\right)=\left[\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right]\cup\left[\frac{\mathrm{1}}{\mathrm{3}},\frac{\mathrm{2}}{\mathrm{3}}\right]\cup\left[\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{3}}{\mathrm{4}}\right]\cup…\cup\left[\mathrm{0},\mathrm{1}\right]=\left[\mathrm{0},\mathrm{1}\right] \\ $$$${are}\:{they}\:{correct} \\ $$$${i}\:{don}'{t}\:{have}\:{any}\:{experience}\:{of}\:{solving}\:{these} \\ $$$${type}\:{of}\:{questions}.\:{don}'{t}\:{even}\:{know}\:{meaning} \\ $$$${of}\:\cup_{{n}=\mathrm{1}} ^{\infty} \\ $$
Commented by Tony Lin last updated on 22/Aug/19
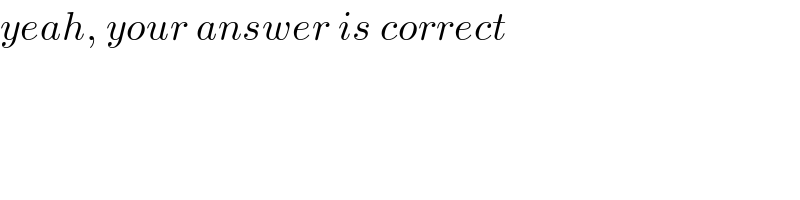
$${yeah},\:{your}\:{answer}\:{is}\:{correct} \\ $$
