1-k-1-C-n-k-

Question Number 141614 by ArielVyny last updated on 21/May/21

$$\Sigma\frac{\mathrm{1}}{{k}+\mathrm{1}}{C}_{{n}} ^{{k}} \:.\: \\ $$

Commented by Dwaipayan Shikari last updated on 21/May/21

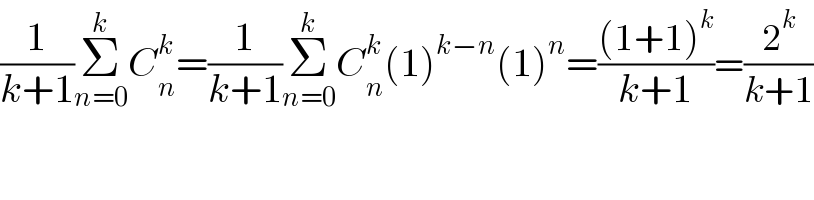
(1/(k+1))Σ_(n=0) ^k C_n ^k =(1/(k+1))Σ_(n=0) ^k C_n ^k (1)^(k−n) (1)^n =(((1+1)^k )/(k+1))=(2^k /(k+1))

$$\frac{\mathrm{1}}{{k}+\mathrm{1}}\underset{{n}=\mathrm{0}} {\overset{{k}} {\sum}}{C}_{{n}} ^{{k}} =\frac{\mathrm{1}}{{k}+\mathrm{1}}\underset{{n}=\mathrm{0}} {\overset{{k}} {\sum}}{C}_{{n}} ^{{k}} \left(\mathrm{1}\right)^{{k}−{n}} \left(\mathrm{1}\right)^{{n}} =\frac{\left(\mathrm{1}+\mathrm{1}\right)^{{k}} }{{k}+\mathrm{1}}=\frac{\mathrm{2}^{{k}} }{{k}+\mathrm{1}} \\ $$

Commented by mathmax by abdo last updated on 21/May/21

$$\mathrm{not}\:\mathrm{correct}\:\mathrm{sir}\:… \\ $$

Answered by mathmax by abdo last updated on 21/May/21

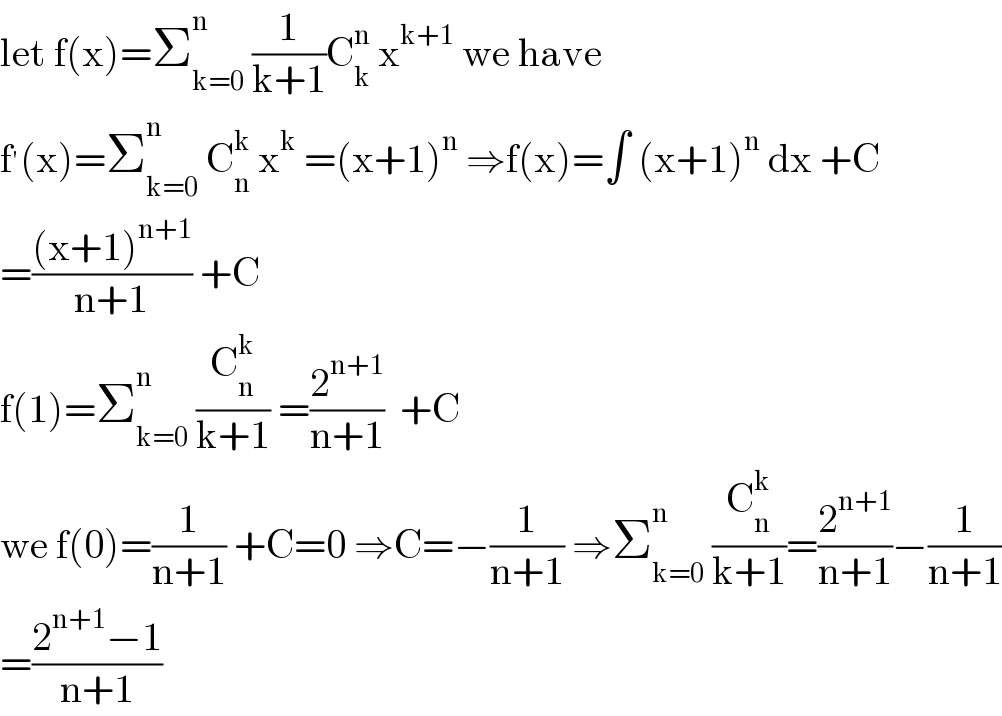
let f(x)=Σ_(k=0) ^n (1/(k+1))C_k ^n x^(k+1) we have f^′ (x)=Σ_(k=0) ^n C_n ^k x^k =(x+1)^n ⇒f(x)=∫ (x+1)^n dx +C =(((x+1)^(n+1) )/(n+1)) +C f(1)=Σ_(k=0) ^n (C_n ^k /(k+1)) =(2^(n+1) /(n+1)) +C we f(0)=(1/(n+1)) +C=0 ⇒C=−(1/(n+1)) ⇒Σ_(k=0) ^n (C_n ^k /(k+1))=(2^(n+1) /(n+1))−(1/(n+1)) =((2^(n+1) −1)/(n+1))

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\mathrm{C}_{\mathrm{k}} ^{\mathrm{n}} \:\mathrm{x}^{\mathrm{k}+\mathrm{1}} \:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \:=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{n}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\int\:\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{dx}\:+\mathrm{C} \\ $$$$=\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:+\mathrm{C} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{k}+\mathrm{1}}\:=\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:\:+\mathrm{C} \\ $$$$\mathrm{we}\:\mathrm{f}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:+\mathrm{C}=\mathrm{0}\:\Rightarrow\mathrm{C}=−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:\Rightarrow\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{k}+\mathrm{1}}=\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$

Commented by ArielVyny last updated on 22/May/21

$${thank}\:{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply