Question Number 141633 by Willson last updated on 21/May/21
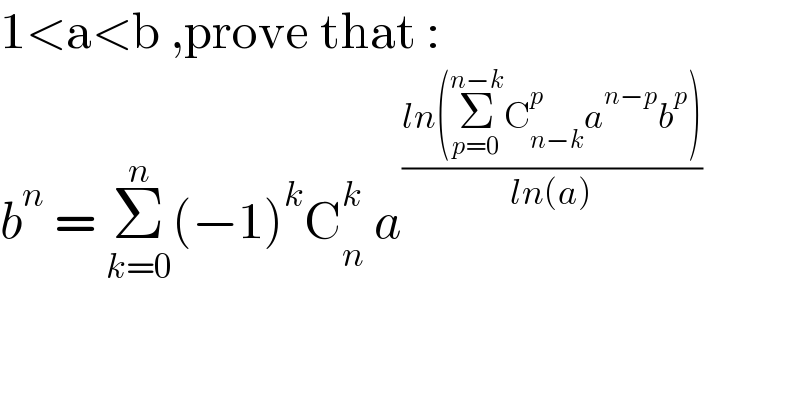
$$\mathrm{1}<\mathrm{a}<\mathrm{b}\:,\mathrm{prove}\:\mathrm{that}\:: \\ $$$${b}^{{n}} \:=\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \mathrm{C}_{{n}} ^{{k}} \:{a}^{\frac{{ln}\left(\underset{{p}=\mathrm{0}} {\overset{{n}−{k}} {\sum}}\mathrm{C}_{{n}−{k}} ^{{p}} {a}^{{n}−{p}} {b}^{{p}} \right)}{{ln}\left({a}\right)}} \\ $$
