Question Number 66462 by mathmax by abdo last updated on 15/Aug/19
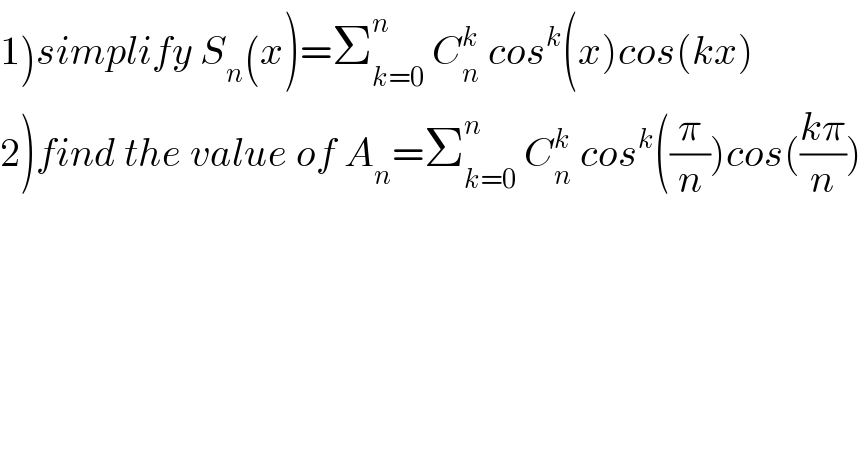
$$\left.\mathrm{1}\right){simplify}\:{S}_{{n}} \left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}^{{k}} \left({x}\right){cos}\left({kx}\right) \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:{A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}^{{k}} \left(\frac{\pi}{{n}}\right){cos}\left(\frac{{k}\pi}{{n}}\right) \\ $$
Commented by mathmax by abdo last updated on 21/Aug/19

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{S}_{{n}} \left({x}\right)={Re}\left(\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}^{{k}} {x}\:{e}^{{ikx}} \right)\:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}^{{k}} {xe}^{{ikx}} \:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \left({e}^{{ix}} {cosx}\right)^{{k}} \:×\mathrm{1}^{{n}−{k}} =\left(\mathrm{1}+{e}^{{ix}} {cosx}\right)^{{n}} \\ $$$$=\left(\mathrm{1}+{cosx}\left\{{cosx}\:+{isinx}\right\}\right)^{{n}} \:=\left(\mathrm{1}+{cos}^{\mathrm{2}} {x}\:+{isinx}\:{cosx}\right)^{{n}} \\ $$$${let}\:{z}\:=\mathrm{1}+{cos}^{\mathrm{2}} {x}\:+{isinx}\:{cosx}\:\Rightarrow\mid{z}\mid=\sqrt{\left(\mathrm{1}+{cos}^{\mathrm{2}} {x}\right)^{\mathrm{2}} +{sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{2}} {x}} \\ $$$$=\sqrt{\mathrm{1}+{cos}^{\mathrm{4}} {x}\:+\mathrm{2}{cos}^{\mathrm{2}} {x}\:+\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right){cos}^{\mathrm{2}} {x}} \\ $$$$=\sqrt{\mathrm{1}+{cos}^{\mathrm{4}} {x}\:+\mathrm{2}{cos}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}−{cos}^{\mathrm{4}} {x}}=\Rightarrow\sqrt{\mathrm{1}+\mathrm{3}{cos}^{\mathrm{2}} {x}}\:\Rightarrow \\ $$$${z}\:=\sqrt{\mathrm{1}+\mathrm{3}{cos}^{\mathrm{2}} {x}}{e}^{{i}\:{arctan}\left(\frac{{sinx}\:{cosx}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}\right)} \\ $$$${we}\:{have}\:\:\frac{{sinxcosx}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}\:=\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right)}\:=\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}+\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}\:=\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{3}+{cos}\left(\mathrm{2}{x}\right)} \\ $$$${and}\:\mathrm{1}+{cos}^{\mathrm{2}} {x}\:=\mathrm{1}+\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\:=\frac{\mathrm{3}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\:\Rightarrow \\ $$$${z}\:=\left(\frac{\mathrm{3}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:{e}^{{i}\:{arctan}\left(\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{3}+{cos}\left(\mathrm{2}{x}\right)}\right)} \:\Rightarrow \\ $$$${z}^{{n}} \:=\left(\frac{\mathrm{3}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right)^{\frac{{n}}{\mathrm{2}}} \:{e}^{{in}\:{arctan}\left(\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{3}+{cos}\left(\mathrm{2}{x}\right)}\right)} \:\Rightarrow \\ $$$${S}_{{n}} \left({x}\right)\:={Re}\left({z}^{{n}} \right)\:=\left(\frac{\mathrm{3}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right)^{\frac{{n}}{\mathrm{2}}} \:{cos}\left({n}\:{arctan}\left(\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{3}+{cos}\left(\mathrm{2}{x}\right)}\right)\right) \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:{cos}^{{k}} \left(\frac{\pi}{{n}}\right)\:{cos}\left(\frac{{k}\pi}{{n}}\right) \\ $$$$={S}_{{n}} \left(\frac{\pi}{{n}}\right)\:=\left(\frac{\mathrm{3}+{cos}\left(\frac{\mathrm{2}\pi}{{n}}\right)}{\mathrm{2}}\right)^{\frac{{n}}{\mathrm{2}}} \:{cos}\left({narctan}\left(\frac{{sin}\left(\frac{\mathrm{2}\pi}{{n}}\right)}{\mathrm{3}+{cos}\left(\frac{\mathrm{2}\pi}{{n}}\right)}\right)\right). \\ $$
