Question Number 73160 by Aditya789 last updated on 07/Nov/19

$$\mathrm{1}+{tanAtan}\frac{{A}}{\mathrm{2}}={tanAcot}\frac{{A}}{\mathrm{2}}−\mathrm{1}={secA} \\ $$
Answered by $@ty@m123 last updated on 07/Nov/19
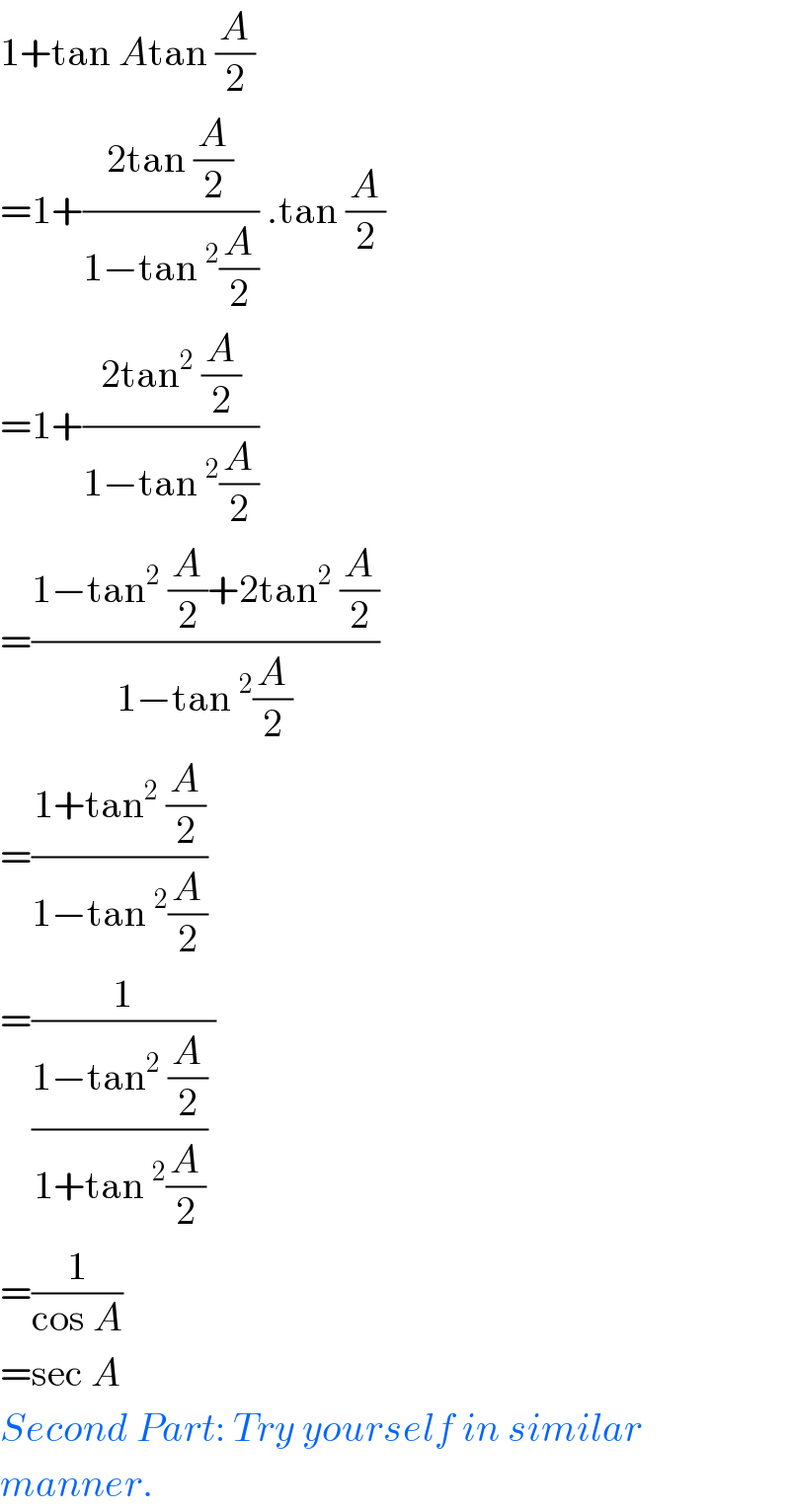
$$\mathrm{1}+\mathrm{tan}\:{A}\mathrm{tan}\:\frac{{A}}{\mathrm{2}} \\ $$$$=\mathrm{1}+\frac{\mathrm{2tan}\:\frac{{A}}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \frac{{A}}{\mathrm{2}}}\:.\mathrm{tan}\:\frac{{A}}{\mathrm{2}} \\ $$$$=\mathrm{1}+\frac{\mathrm{2tan}^{\mathrm{2}} \:\frac{{A}}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \frac{{A}}{\mathrm{2}}}\: \\ $$$$=\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{{A}}{\mathrm{2}}+\mathrm{2tan}^{\mathrm{2}} \:\frac{{A}}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \frac{{A}}{\mathrm{2}}}\: \\ $$$$=\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\frac{{A}}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \frac{{A}}{\mathrm{2}}}\: \\ $$$$=\frac{\mathrm{1}}{\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{{A}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \frac{{A}}{\mathrm{2}}}\:} \\ $$$$=\frac{\mathrm{1}}{\mathrm{cos}\:{A}} \\ $$$$=\mathrm{sec}\:{A} \\ $$$${Second}\:{Part}:\:{Try}\:{yourself}\:{in}\:{similar} \\ $$$${manner}. \\ $$
