Question Number 68368 by naka3546 last updated on 09/Sep/19
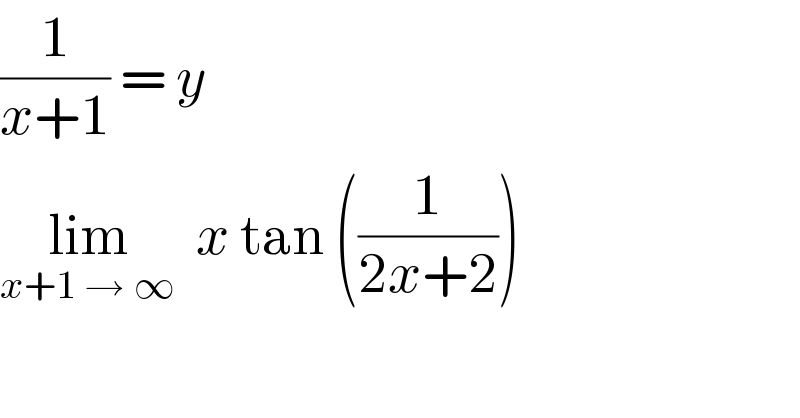
$$\frac{\mathrm{1}}{{x}+\mathrm{1}}\:=\:{y} \\ $$$$\underset{{x}+\mathrm{1}\:\rightarrow\:\infty} {\mathrm{lim}}\:\:{x}\:\mathrm{tan}\:\left(\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}}\right) \\ $$
Commented by kaivan.ahmadi last updated on 09/Sep/19
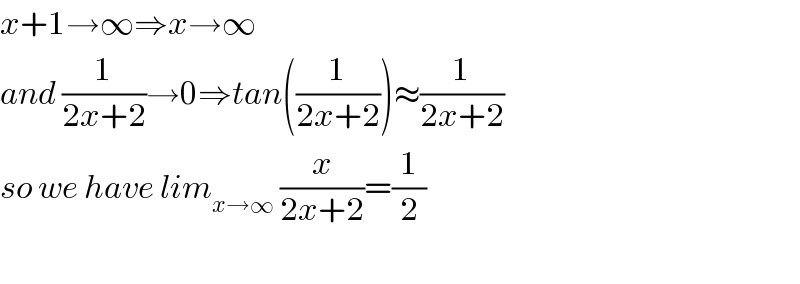
$${x}+\mathrm{1}\rightarrow\infty\Rightarrow{x}\rightarrow\infty \\ $$$${and}\:\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}}\rightarrow\mathrm{0}\Rightarrow{tan}\left(\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}}\right)\approx\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}} \\ $$$${so}\:{we}\:{have}\:{lim}_{{x}\rightarrow\infty} \:\frac{{x}}{\mathrm{2}{x}+\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by Tanmay chaudhury last updated on 09/Sep/19
![lim_(y→0) ((1/y)−1)tan((y/2)) lim_(y→0) [(1/y)×sin((y/2))×(1/(cos((y/2))))−tan((y/2))] lim_(y→0) ((sin((y/2)))/(((y/2))×2))×(1/(cos((y/2))))−lim_(y→0) tan((y/2)) =(1/2)×(1/1)−0 =(1/2)](https://www.tinkutara.com/question/Q68380.png)
$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{{y}}−\mathrm{1}\right){tan}\left(\frac{{y}}{\mathrm{2}}\right) \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{\mathrm{1}}{{y}}×{sin}\left(\frac{{y}}{\mathrm{2}}\right)×\frac{\mathrm{1}}{{cos}\left(\frac{{y}}{\mathrm{2}}\right)}−{tan}\left(\frac{{y}}{\mathrm{2}}\right)\right] \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{sin}\left(\frac{{y}}{\mathrm{2}}\right)}{\left(\frac{{y}}{\mathrm{2}}\right)×\mathrm{2}}×\frac{\mathrm{1}}{{cos}\left(\frac{{y}}{\mathrm{2}}\right)}−\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{tan}\left(\frac{{y}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{1}}−\mathrm{0} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
