Question Number 71175 by 20190927 last updated on 12/Oct/19
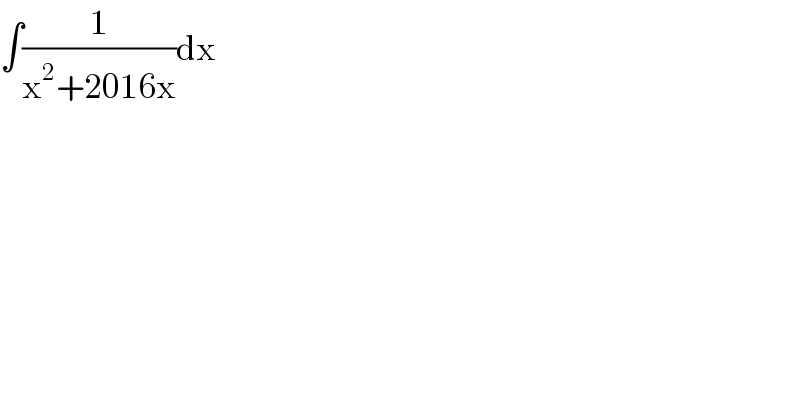
$$\int\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2016x}}\mathrm{dx} \\ $$
Commented by Prithwish sen last updated on 12/Oct/19
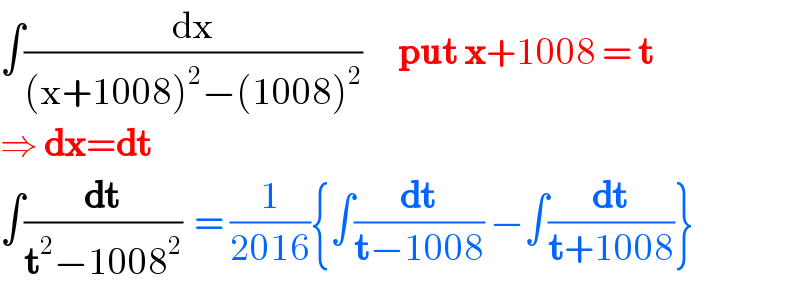
$$\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1008}\right)^{\mathrm{2}} −\left(\mathrm{1008}\right)^{\mathrm{2}} }\:\:\:\:\:\:\boldsymbol{\mathrm{put}}\:\boldsymbol{\mathrm{x}}+\mathrm{1008}\:=\:\boldsymbol{\mathrm{t}} \\ $$$$\Rightarrow\:\boldsymbol{\mathrm{dx}}=\boldsymbol{\mathrm{dt}} \\ $$$$\int\frac{\boldsymbol{\mathrm{dt}}}{\boldsymbol{\mathrm{t}}^{\mathrm{2}} −\mathrm{1008}^{\mathrm{2}} }\:\:=\:\frac{\mathrm{1}}{\mathrm{2016}}\left\{\int\frac{\boldsymbol{\mathrm{dt}}}{\boldsymbol{\mathrm{t}}−\mathrm{1008}}\:−\int\frac{\boldsymbol{\mathrm{dt}}}{\boldsymbol{\mathrm{t}}+\mathrm{1008}}\right\} \\ $$
Commented by Prithwish sen last updated on 12/Oct/19
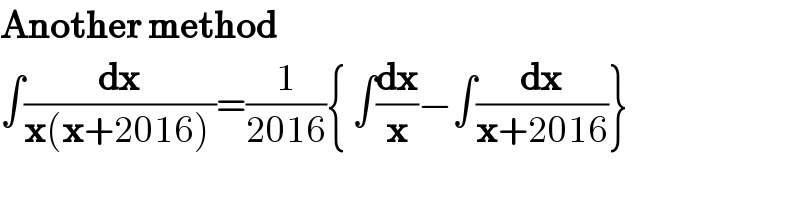
$$\boldsymbol{\mathrm{Another}}\:\boldsymbol{\mathrm{method}} \\ $$$$\int\frac{\boldsymbol{\mathrm{dx}}}{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}+\mathrm{2016}\right)\:}=\frac{\mathrm{1}}{\mathrm{2016}}\left\{\:\int\frac{\boldsymbol{\mathrm{dx}}}{\boldsymbol{\mathrm{x}}}−\int\frac{\boldsymbol{\mathrm{dx}}}{\boldsymbol{\mathrm{x}}+\mathrm{2016}}\right\} \\ $$
Commented by 20190927 last updated on 13/Oct/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by petrochengula last updated on 13/Oct/19
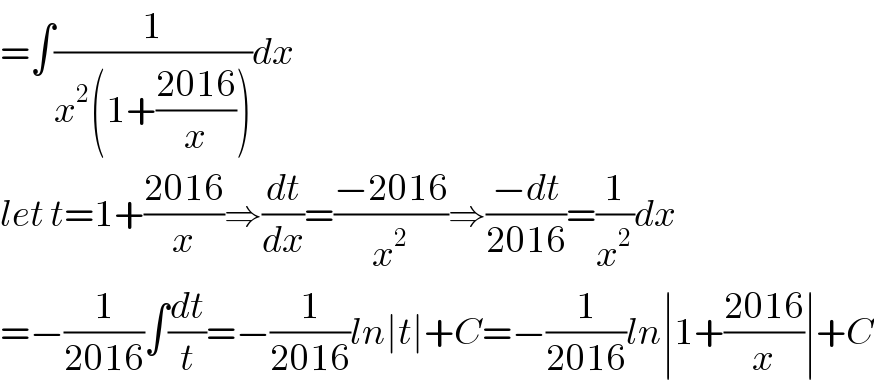
$$=\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{2016}}{{x}}\right)}{dx} \\ $$$${let}\:{t}=\mathrm{1}+\frac{\mathrm{2016}}{{x}}\Rightarrow\frac{{dt}}{{dx}}=\frac{−\mathrm{2016}}{{x}^{\mathrm{2}} }\Rightarrow\frac{−{dt}}{\mathrm{2016}}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2016}}\int\frac{{dt}}{{t}}=−\frac{\mathrm{1}}{\mathrm{2016}}{ln}\mid{t}\mid+{C}=−\frac{\mathrm{1}}{\mathrm{2016}}{ln}\mid\mathrm{1}+\frac{\mathrm{2016}}{{x}}\mid+{C} \\ $$
Commented by 20190927 last updated on 13/Oct/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by Prithwish sen last updated on 13/Oct/19

$$\mathrm{Amazing}!\:\mathrm{Sir}.\: \\ $$
