1-x-2-25-x-2-dx-

Question Number 135498 by aurpeyz last updated on 13/Mar/21

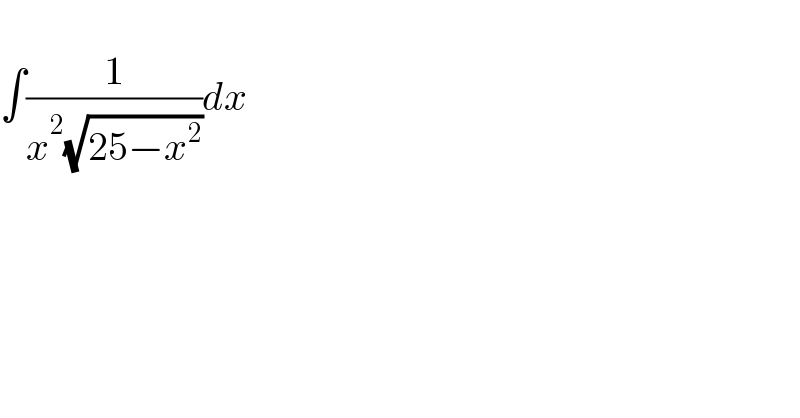
$$ \\ $$$$\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} \sqrt{\mathrm{25}−{x}^{\mathrm{2}} }}{dx} \\ $$

Answered by john_santu last updated on 13/Mar/21

F = ∫ (dx/(x^3 (√(25x^(−2) −1)))) dx = ∫ (x^(−3) /( (√(25x^(−2) −1)))) dx change of variable let (√(25x^(−2) −1)) = w ⇒−50x^(−3) dx = 2w dw ⇒x^(−3) dx =−(1/(25))w dw F = −(1/(25))∫ ((w dw)/w) = −(1/(25))∫ dw F = −(1/(25)) w + c F = −(1/(25)) (√((25−x^2 )/x^2 )) + c F = −((√(25−x^2 ))/(25x)) + c

$$\mathscr{F}\:=\:\int\:\frac{{dx}}{{x}^{\mathrm{3}} \:\sqrt{\mathrm{25}{x}^{−\mathrm{2}} −\mathrm{1}}}\:{dx}\:=\:\int\:\frac{{x}^{−\mathrm{3}} }{\:\sqrt{\mathrm{25}{x}^{−\mathrm{2}} −\mathrm{1}}}\:{dx} \\ $$$${change}\:{of}\:{variable} \\ $$$${let}\:\sqrt{\mathrm{25}{x}^{−\mathrm{2}} −\mathrm{1}}\:=\:{w}\:\Rightarrow−\mathrm{50}{x}^{−\mathrm{3}} \:{dx}\:=\:\mathrm{2}{w}\:{dw} \\ $$$$\Rightarrow{x}^{−\mathrm{3}} \:{dx}\:=−\frac{\mathrm{1}}{\mathrm{25}}{w}\:{dw} \\ $$$$\mathscr{F}\:=\:−\frac{\mathrm{1}}{\mathrm{25}}\int\:\frac{{w}\:{dw}}{{w}}\:=\:−\frac{\mathrm{1}}{\mathrm{25}}\int\:{dw} \\ $$$$\mathscr{F}\:=\:−\frac{\mathrm{1}}{\mathrm{25}}\:{w}\:+\:{c} \\ $$$$\mathscr{F}\:=\:−\frac{\mathrm{1}}{\mathrm{25}}\:\sqrt{\frac{\mathrm{25}−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}\:+\:{c}\: \\ $$$$\mathscr{F}\:=\:−\frac{\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }}{\mathrm{25}{x}}\:+\:{c}\: \\ $$

Commented by aurpeyz last updated on 15/Mar/21

$${thanks} \\ $$

Commented by aurpeyz last updated on 15/Mar/21

$${thanks}\:{allt} \\ $$

Answered by mathmax by abdo last updated on 13/Mar/21

I=∫ (dx/(x^2 (√(25−x^2 )))) we do the changement x=5sint ⇒I =∫ ((5cost dt)/(5(5sint)^2 cost)) =(1/(25))∫ (dt/(sin^2 t)) =(2/(25))∫ (dt/(1−cos(2t))) =_(tant =u) (2/(25))∫ (du/((1+u^2 )(1−((1−u^2 )/(1+u^2 ))))) =(2/(25))∫ (du/(1+u^2 −1+u^2 )) =(2/(25))∫ (du/(2u^2 )) =−(1/(25u)) +c =−(1/(25tant)) +c =−((cost)/(25 sint)) +c =−((√(1−sin^2 t))/(5(5sint))) +c =−((√(1−(x^2 /(25))))/(5x)) +c

$$\mathrm{I}=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}=\mathrm{5sint} \\ $$$$\Rightarrow\mathrm{I}\:=\int\:\:\frac{\mathrm{5cost}\:\mathrm{dt}}{\mathrm{5}\left(\mathrm{5sint}\right)^{\mathrm{2}} \mathrm{cost}}\:=\frac{\mathrm{1}}{\mathrm{25}}\int\:\:\frac{\mathrm{dt}}{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}\:=\frac{\mathrm{2}}{\mathrm{25}}\int\:\:\frac{\mathrm{dt}}{\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)} \\ $$$$=_{\mathrm{tant}\:=\mathrm{u}} \:\:\:\frac{\mathrm{2}}{\mathrm{25}}\int\:\:\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)}\:=\frac{\mathrm{2}}{\mathrm{25}}\int\:\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} −\mathrm{1}+\mathrm{u}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{25}}\int\:\:\frac{\mathrm{du}}{\mathrm{2u}^{\mathrm{2}} }\:=−\frac{\mathrm{1}}{\mathrm{25u}}\:+\mathrm{c}\:=−\frac{\mathrm{1}}{\mathrm{25tant}}\:+\mathrm{c}\:\:=−\frac{\mathrm{cost}}{\mathrm{25}\:\mathrm{sint}}\:+\mathrm{c} \\ $$$$=−\frac{\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{t}}}{\mathrm{5}\left(\mathrm{5sint}\right)}\:+\mathrm{c}\:=−\frac{\sqrt{\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{25}}}}{\mathrm{5x}}\:+\mathrm{c}\:\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply